什么选择物理不可克隆函数（PUF）？ 什么选择物理不可克隆函数（PUF）？20年前，数字安全只在银行卡或支付终端等专用电子设备上实现。今天，每个人都在使用以 "https://"标志的安全互联网连接到银行，我们都希望我们用智能手机操作的信息能够得到保护。加密或数字签名等加密技术已经被部署以满足这些要求。因此，越来越多的ASIC、微控制器和SoC都嵌入了硬件加密加速器或软件加密库。物联网（IoT）的兴起将加快对加密的需求。现在就让我们讨论密码学的普及情况。因为在现代密码学中算法都是公开和标准化的，使得加密技术的普及成为可能。公开算法的直接后果是密钥成为最有价值的资产，因此它们必须得到强有力的保护。历史上，第一个被设计用来保护密钥的集成电路(IC)是智能卡。随着人们对数字安全需求的日益增长，加密已经在越来越多的芯片（如通用微控制器）中得到应用，但密钥的保护一直是一个挑战。今天我们可以看到有以下几种方案：l未未实施特定保护。这种情况不应该发生，但不幸的是，这种情况还是会发生!l内部逻辑保护，如TrustZone™. 密钥可以防止逻辑攻击（如恶意软件），但不能防止物理攻击。l电路内逻辑和物理保护。l密钥存储在位于主处理器外部独立的被称为“安全元件”专用集成电路中。在集成电路(IC)中，密钥保护方案的选择取决于许多因素:lIC制造技术的可用性:非易失性存储器如EEPROM或Flash的存在直接影响到密钥的物理保护方式l市场要求:在集成电路中实现的安全级别取决于其最终用途lIC设计师专有技术:硬件保护单元的设计仍然是专家的事l上市时间l开发成本l单位成本(额外的芯片面积)人们可能认为，在大多数情况下，物理保护是没有必要的。但事实已不再是这样，因为与失效分析技术相关的自动反向工程已经使物理攻击变得可负担得起[1]。传统的安全密钥存储的设计方式包括将密钥存储在非易失性存储器（OTP、EEPROM或Flash）中，并实现布局反击措施或混淆，如芯片屏蔽、总线加扰或伪过孔等[2]。一个更稳健的解决方案依赖于通过主密钥对存储器进行加密，但随后的挑战是对主密钥本身的保护，我们又回到了最初的挑战。以这种方法是有效的并且已通过通用标准之类的认证。典型的如EAL4 +认证（或更高版本AVA_VAN.5），用来对IC的物理攻击抵抗力进行评级。这个评级是基于成功进行攻击的难度来判定，主要基于以下要求：l专业水平l时间l设备成本一般来说，如果上述标准的综合水平与攻击者所能获得的利益相比足够高，那么该实现就被认为是有效的，尽管事实上，只要有足够的时间、专业知识和预算，仍然有可能检索到密钥。上面列出的混淆方法的主要缺点是它们同样需要高度的专业知识，而只有少数IC设计人员才能掌握。这些解决方案无法轻易获得，因此在许多情况下并不适用。我们将看到，以IP形式交付的物理不可克隆功能(PUF)即使对非安全专家来说，也能实现最高级别的安全性。PUF和传统技术之间的一个基本区别是PUF本质上不受逆向工程技术的影响。PUF解决的另一个挑战是需要在密钥注入IC之前保护它们:传统方法需要在制造过程的某些步骤中注入密钥，这可能发生在晶圆测试（CP）、IC终测（FT）或PCB制造过程中。但无论选择什么步骤，秘钥必须通过测试或制造设备注入到IC中，因此安全的周边环境是必需的。安全地注入密钥是一个像给银行卡加密操作的过程，但对于医疗、工业或消费品来说，这可能是负担不起的。通常情况下，制造工作由位于偏远地区的分包商负责，而且要求分包商提供安全设施是具有挑战性的，因此必须投资访问控制设备、编写程序和定期进行审计。PUF用例私钥和秘钥存储如上所述，密钥存储通常是主要问题。 PUF生成的密钥用于片上非易失性存储器（例如EEPROM，Flash 或OTP）中建立安全库。 图1使用PUF实施高度安全的密钥库 软件IP保护一些用于医学诊断或生命体征测量的算法是多年积累和研发的结果。因此，它们是极有价值的资产，应该得到强有力的保护。而PUF生成的密钥可以通过加密保护这些软件IP。 图2基于PUF的软件IP保护设备认证身份验证是连接设备的首要安全要求之一，即确保设备是真实的。最安全的方法是执行挑战应答认证（challenge-response authentication）。该方案将随机数（挑战）发送到要进行身份验证的设备，然后该设备使用其私钥对挑战进行签名。同样，私钥必须受到严格保护。PUF原理与传统技术（涉及定制设计）相比，用于实现安全存储且保护等级更高的交钥匙解决方案听起来像是安全圣杯。我们将看到一个健壮且易于集成的PUF现在已成为现实。PUF依赖于微小的制造差异。制造差异会导致设备不一致。 这个想法是，设计上完全相同的两个（或多个）设备实际上将具有不同的电性能参数。电性能参数的差异是无法预测的，无法通过光学或SEM观察来估计。 图3 PUF晶体管对的原理图和布局图在上面的示意图中，尽管两个晶体管A和B在设计上是相同的，但在实践中它们始终具有略微不同的物理特征， 如作为阈值电压（VT），漏源电流（IDS）或漏源电阻（RDSON）等参数是不同的。 设计人员可以选择不同的参数来构建其PUF。 为了为了在本文中保持通用，我们将使用 PA和 PB来表示不同的参数，需要注意的是它可以是任何晶体管参数或它们的组合。由于晶体管A和B在设计上是相同的，因此无论是通过仿真还是逆向工程都不可能预测每个结构的PA>PB还是PA<PB。 如果我们武断的认为PA> PB生成“ 0”而PA <PB生成“ 1”，则无法猜测该对晶体管在被探测时生成的是“ 0”还是“ 1”。通过将该结构重复N次，我们可以生成N位不可预测的数据流。其实我们刚刚已经设计了一个物理不可克隆函数。 图4多个实例晶体管对创建的不可预测的比特流 PUF挑战如图所示，实现一系列多个晶体管实例（instance）或任何其他器件并不是什么大事。因此基于此原理构建PUF似乎非常容易。但其实并不是！如介绍中所述，PUF是基于硅制造中的微小变化。在我们的例子中，这些微小的变化转换成PA > PB或PA < PB。 但是由于制造偏差很小，因此△P=PA-PB之差也是如此。由于△P小，因此必须进行高精度测量。 如果测量不准的话，“ 0”很容易翻转为“ 1”（反之亦然），那么PUF不能用于生成密钥。因此，测量精度是一个重大挑战。更糟糕的是，△P通常对老化、温度、工艺和电源变化很敏感。△P本质上很小而且是随机分布的，因此最低的△P的单元在不同温度下使用时会有发生翻转的趋势。我们可以将这些单元视为“弱”，而将具有较高△P的单元视为“强”，后者对变化的敏感性较小。像在存储器设计中那样，添加额外的或冗余单元是将弱单元替换为强单元的一种有效途径。 图5 弱单元强单元的特性 虽然实现PUF元素相对简单，但要获得上述参数的稳定性是一个真正的挑战。有几种技术可以建立稳定的PUF：l 选择合适的参数（VT、IDS、RDSON）以便容易地进行高精度测量；l 冗余：设计更多的PUF元件来消除“弱”实例。 同样这里需要仔细的估计弱单元的数量。 没有足够的冗余单元会导致良率问题，而增加太多的冗余单元会使PUF的硅面积过大。这两个问题都会增加实际的芯片成本。l 纠错：假设不稳定单元的百分比足够低，实施适当的纠错机制（例如汉明编码）将会“修复”密钥。但局限性在于你需要对潜在的有缺陷的PUF单元进行相当有力的估算。除了测量精度之外，使PUF方案具有价值的实际上是纠错或冗余方案的效率成本。和其他密钥生成过程一样，可靠性是必不可少的，PUF的不可预测性和唯一性也是人们所期望的。不可预测性意味着在给定的芯片上，即使知道PUF对一系列挑战的响应，也无法猜测对下一个挑战的响应。唯一性是给定的PUF设计能够针对每个芯片和相同的挑战生成唯一的响应能力[3]。INVIA PUF：灵活、可靠、安全的解决方案架构我们的PUF基于晶体管失配，并且包括关键的多样化特性。一个实例可提供128个安全位，并且可由经过验证的多样化工艺而生成多个密钥。 图6 INVIA  PUF架构 老化韧性让我们看看已知的老化现象如何影响INVIA PUF技术和其他PUF技术 老化现象 描述  对 INVIA PUF的影响 对其他技术的影响热载流子注入(HCI) NMOS晶体管的栅极电介质中捕获的载流子会产生Vt和gm漂移 在125°C下放置10年，PUF晶体管的Vt和gm变化小于1％ 中等影响-晶体管在低Vds下工作显著影响-晶体管在高Vds下工作介质层时变击穿(TDDB) 氧化层击穿是由电子隧穿电流引起的 影响非常有限，因为我们的PUF单元的最大工作电压为〜0.5 Vdd 显著影响-MOSFET晶体管的工作电压接近最大规定的工作电压有限影响-正常电压负偏压温度不稳定性(NBTI) 由于正电荷在栅极下方的氧化物半导体边界处捕获，Vt和gm发生偏移。当Vg <Vs时会发生这种现象，这在导通的PMOS晶体管中很普遍 没有影响：-我们的技术仅基于NMOS晶体管-PUF晶体管在Vg> Vs下工作 基于SRAM的PUF技术对NBTI敏感，因为它们使用Vg<Vs的PMOS晶体管上表显示，我们的PUF具有与生俱来的抗老化特性。为了获得更高的可靠性而增加了冗余。如前所述，我们实现了比所需数量更多的单元来消除了弱单元。我们为PUF建立的模型使我们能够设置正确的区分阈值，以消除不可靠的PUF元素。实验已验证了模型的正确性并进行了高温工作寿命试验(HTOL)。模拟结构允许在老化后进行参数漂移测量，这比Go/No-go测试提供了更高的置信度。此外，PUF晶体管只有在被有效感知且在极短的时间内才通电。与持续供电的存储阵列PUF结构相比这自然减少了应力等级。熵除了消除弱单元之外，还建立辅助数据来增强针对外部参数变化和老化的鲁棒性。这可能导致熵损失。INVIA PUF在17亿比特位上显示出一个极好的熵>0.998建模INVIA设计的PUF IP不仅要耐高温、电压和工艺变化而且还能够对其建模，避免了任何形式的黑魔法。因为PUF本质上依赖于非常随机的现象，所以人们可能会通过实验和特性描述来实现PUF单元并凭经验判断其是否工作，然后发布相关IP产品。这可能有用但不能提供最高层次的信任。拥有PUF模型具有以下明显的优势：l方案具有可信性。确保密钥的构建具有足够的熵和健壮性是非常基本的要求。l结果可预测性。将方案移植到其他工艺节点变得更加容易。lIP可以通过认证 结论使用具有可靠性、不可预测性和唯一性保证的PUF IP，即使对于不是安全专家的设计人员，也可以为ASIC或SoC提供最高级别的安全性。 参考文献References[1] e. a. S. Quadir, 《A survey on chip to system reverse engineering》 ACM Journalon Emerging Technologies in Computing Systems, April 2016.[2] D. F. M. M. T. Q. S. Huanyu Wang, 《Probing Attacks on Integrated Circuits:Challenges and Research Opportunities》, IEEE Design & Test , October 2017.[3] M. Bhargava, 《Reliable, Secure, Efficient Physical Unclonable Functions. Thesis》,01 May 2013. [En ligne]. Available: https://doi.org/10.1184/R1/6721310.v1.

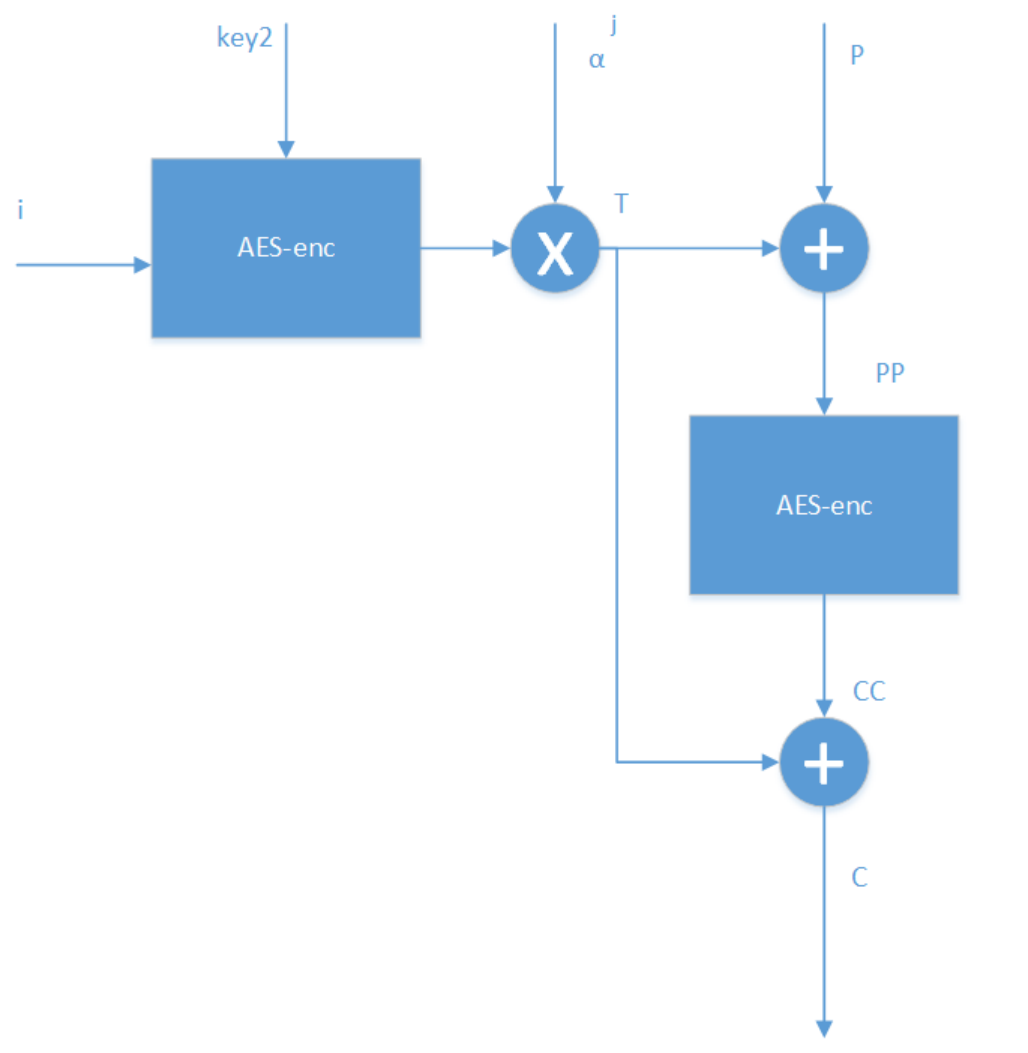
XTS-AES模式主要是解决什么问题，是怎样解决的? XTS-AES模式主要是解决什么问题，是怎样解决的?作者：蒋伟伟链接：https://www.zhihu.com/question/26452995/answer/142440391来源：知乎著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。XTS即基于XEX(XOR-ENCRYPT-XOR)的密文窃取算法的可调整的密码本模式（Tweakable Codebook mode），该算法主要用于以数据单元（包括扇区、逻辑磁盘块等）为基础结构的存储设备中静止状态数据的加密。以上是官方的解释，谈一下我的理解。我们都知道磁盘上的数据是有一定格式的，比如一个扇区是512字节，磁盘加密直接要对写入扇区的明文进行加密，记录在磁盘扇区上的是相应的密文。而我们通过传统的AES加密方法，比如CBC加密模式，密文须包含一个128bit的初始向量。那么问题来了，我们岂不是要腾出额外的128个bit专门存储初始向量？这样做是增加了磁盘的开销，而且明文和密文在扇区上的存储也不是一一对应的，这给磁盘底层的加密实现带来很大的麻烦。更为关键的是，传统的加密算法，更改密匙非常不便，一旦更改，就意味着要重新进行密匙扩展算法，对磁盘来说要增加很大的开销，同时还要担心密匙泄露的问题。在这种情况下，针对磁盘加密的特点，2002年，Moses Liskov，Ronald L.Rivest, David Wagner,首次提出了可调整的分组密码这个概念，跟传统的分组密码相比，除了密匙和明文这两个输入外，还引入另外一个输入---tweak，即可调整值。这样做的好处是，在不更改密匙的情况下，仅仅改变tweak值，就可以给加密系统提供多变性，既减少了磁盘的开销，也不怕密匙泄露，因为tweak值是公开的，就算泄露了tweak值，如果不知道密匙，是无法破解系统的。而且，这种算法，不需要初始向量，也就避免我们上面所述的明文和密文在扇区上的存储不对应的问题。XTS-AES算法是基于以上思想，被IEEE采用的一个标准。简单介绍下其原理，以传输单个128bit数据块为例：i为128-bit调整值，j为128-bit数据块在数据单元中的位置值,C为128-bit密文数据块。AES-enc为标准AES算法，key2为调整值密匙，key1为数据密匙，模乘操作中 α为GF(2^128)域中对应于多项式x的本源。计算的步骤顺序如下：T <---- AES-enc(key2,i) ⓧ (α^j );PP <----P⊕Thttp://3.CC<---AES-enc(Key1,PP)C<--CC⊕T需要指出的是，j代表数据块在数据单元里的index，比如256个bit数据块，那么 0bit-127bit的j=1，128bit-256bit 的j=2。j 的引入，是让各个数据块的加密保持独立。Disk encryption theoryFrom Wikipedia, the free encyclopediaJump to navigationJump to searchDisk encryption is a special case of data at rest protection when the storage medium is a sector-addressable device (e.g., a hard disk). This article presents cryptographic aspects of the problem. For an overview, see disk encryption. For discussion of different software packages and hardware devices devoted to this problem, see disk encryption software and disk encryption hardware.Contents1Problem definition2Block cipher-based modes2.1Cipher-block chaining (CBC)2.1.1Encrypted salt-sector initialization vector (ESSIV)2.1.2Malleability attack2.2Liskov, Rivest, and Wagner (LRW)2.3Xor–encrypt–xor (XEX)2.3.1XEX-based tweaked-codebook mode with ciphertext stealing (XTS)2.3.2XTS weaknesses2.4CBC–mask–CBC (CMC) and ECB–mask–ECB (EME)3Patents4See also5References6Further reading7External linksProblem definition[edit]Disk encryption methods aim to provide three distinct properties:1.The data on the disk should remain confidential.2.Data retrieval and storage should both be fast operations, no matter where on the disk the data is stored.3.The encryption method should not waste disk space (i.e., the amount of storage used for encrypted data should not be significantly larger than the size of plaintext).The first property requires defining an adversary from whom the data is being kept confidential. The strongest adversaries studied in the field of disk encryption have these abilities:1.they can read the raw contents of the disk at any time;2.they can request the disk to encrypt and store arbitrary files of their choosing;3.and they can modify unused sectors on the disk and then request their decryption.A method provides good confidentiality if the only information such an adversary can determine over time is whether the data in a sector has or has not changed since the last time they looked.The second property requires dividing the disk into several sectors, usually 512 bytes (4096 bits) long, which are encrypted and decrypted independently of each other. In turn, if the data is to stay confidential, the encryption method must be tweakable; no two sectors should be processed in exactly the same way. Otherwise, the adversary could decrypt any sector of the disk by copying it to an unused sector of the disk and requesting its decryption.The third property is generally non-controversial. However, it indirectly prohibits the use of stream ciphers, since stream ciphers require, for their security, that the same initial state not be used twice (which would be the case if a sector is updated with different data); thus this would require an encryption method to store separate initial states for every sector on disk—seemingly a waste of space. The alternative, a block cipher, is limited to a certain block size (usually 128 or 256 bits). Because of this, disk encryption chiefly studies chaining modes, which expand the encryption block length to cover a whole disk sector. The considerations already listed make several well-known chaining modes unsuitable: ECB mode, which cannot be tweaked, and modes that turn block ciphers into stream ciphers, such as the CTR mode.These three properties do not provide any assurance of disk integrity; that is, they don't tell you whether an adversary has been modifying your ciphertext. In part, this is because an absolute assurance of disk integrity is impossible: no matter what, an adversary could always revert the entire disk to a prior state, circumventing any such checks. If some non-absolute level of disk integrity is desired, it can be achieved within the encrypted disk on a file-by-file basis using message authentication codes.Block cipher-based modes[edit]Like most encryption schemes, block cipher-based disk encryption makes use of modes of operation, which allow encrypting larger amounts of data than the ciphers' block-size (typically 128 bits). Modes are therefore rules on how to repeatedly apply the ciphers' single-block operations.Cipher-block chaining (CBC)[edit]Main article: Cipher-block chainingCipher-block chaining (CBC) is a common chaining mode in which the previous block's ciphertext is xored with the current block's plaintext before encryption:Since there isn't a "previous block's ciphertext" for the first block, an initialization vector (IV) must be used as . This, in turn, makes CBC tweakable in some ways.CBC suffers from some problems. For example, if the IVs are predictable, then an adversary may leave a "watermark" on the disk, i.e., store a specially created file or combination of files identifiable even after encryption. The exact method of constructing the watermark depends on the exact function providing the IVs, but the general recipe is to create two encrypted sectors with identical first blocks  and ; these two are then related to each other by . Thus the encryption of  is identical to the encryption of , leaving a watermark on the disk. The exact pattern of "same-different-same-different" on disk can then be altered to make the watermark unique to a given file.To protect against the watermarking attack, a cipher or a hash function is used to generate the IVs from the key and the current sector number, so that an adversary cannot predict the IVs. In particular, the ESSIV approach uses a block cipher in CTR mode to generate the IVs.Encrypted salt-sector initialization vector (ESSIV)[edit]ESSIV[1] is a method for generating initialization vectors for block encryption to use in disk encryption. The usual methods for generating IVs are predictable sequences of numbers based on, for example, time stamp or sector number, and prevents certain attacks such as a watermarking attack. ESSIV prevents such attacks by generating IVs from a combination of the sector number SN with the hash of the key. It is the combination with the key in form of a hash that makes the IV unpredictable.ESSIV was designed by Clemens Fruhwirth and has been integrated into the Linux kernel since version 2.6.10, though a similar scheme has been used to generate IVs for OpenBSD's swap encryption since 2000.[2]ESSIV is supported as an option by the dm-crypt[3] and FreeOTFE disk encryption systems.Malleability attack[edit]While CBC (with or without ESSIV) ensures confidentiality, it does not ensure integrity of the encrypted data. If the plaintext is known to the adversary, it is possible to change every second plaintext block to a value chosen by the attacker, while the blocks in between are changed to random values. This can be used for practical attacks on disk encryption in CBC or CBC-ESSIV mode.[4]Liskov, Rivest, and Wagner (LRW)[edit]In order to prevent such elaborate attacks, different modes of operation were introduced: tweakable narrow-block encryption (LRW and XEX) and wide-block encryption (CMC and EME).Whereas a purpose of a usual block cipher  is to mimic a random permutation for any secret key , the purpose of tweakable encryption is to mimic a random permutation for any secret key  and any known tweak . The tweakable narrow-block encryption (LRW)[5] is an instantiation of the mode of operations introduced by Liskov, Rivest, and Wagner[6] (see Theorem 2). This mode uses two keys:  is the key for the block cipher and  is an additional key of the same size as block. For example, for AES with a 256-bit key,  is a 256-bit number and  is a 128-bit number. Encrypting block  with logical index (tweak)  uses the following formula:Here multiplication  and addition  are performed in the finite field ( for AES). With some precomputation, only a single multiplication per sector is required (note that addition in a binary finite field is a simple bitwise addition, also known as xor): , where  are precomputed for all possible values of . This mode of operation needs only a single encryption per block and protects against all the above attacks except a minor leak: if the user changes a single plaintext block in a sector then only a single ciphertext block changes. (Note that this is not the same leak the ECB mode has: with LRW mode equal plaintexts in different positions are encrypted to different ciphertexts.)Some security concerns exist with LRW, and this mode of operation has now been replaced by XTS.LRW is employed by BestCrypt and supported as an option for dm-crypt and FreeOTFE disk encryption systems.Xor–encrypt–xor (XEX)[edit]Main article: Xor–encrypt–xorAnother tweakable encryption mode, XEX (xor–encrypt–xor), was designed by Rogaway[7] to allow efficient processing of consecutive blocks (with respect to the cipher used) within one data unit (e.g., a disk sector). The tweak is represented as a combination of the sector address and index of the block within the sector (the original XEX mode proposed by Rogaway[7] allows several indices). The ciphertext, , is obtained using:where: is the plaintext, is the number of the sector, is the primitive element of  defined by polynomial ; i.e., the number 2, is the number of the block within the sector.The basic operations of the LRW mode (AES cipher and Galois field multiplication) are the same as the ones used in the Galois/Counter Mode (GCM), thus permitting a compact implementation of the universal LRW/XEX/GCM hardware.XEX has a weakness.[8]XEX-based tweaked-codebook mode with ciphertext stealing (XTS)[edit]Ciphertext stealing provides support for sectors with size not divisible by block size, for example, 520-byte sectors and 16-byte blocks. XTS-AES was standardized on 2007-12-19[9] as IEEE P1619.[10] The standard supports using a different key for the IV encryption than for the block encryption; this is contrary to the intent of XEX and seems to be rooted in a misinterpretation of the original XEX paper, but does not harm security.11 As a result, users wanting AES-256 and AES-128 encryption must supply 512 bits and 256 bits of key respectively.On January 27, 2010, NIST released Special Publication (SP) 800-38E[12] in final form. SP 800-38E is a recommendation for the XTS-AES mode of operation, as standardized by IEEE Std 1619-2007, for cryptographic modules. The publication approves the XTS-AES mode of the AES algorithm by reference to the IEEE Std 1619-2007, subject to one additional requirement, which limits the maximum size of each encrypted data unit (typically a sector or disk block) to 220 AES blocks. According to SP 800-38E, "In the absence of authentication or access control, XTS-AES provides more protection than the other approved confidentiality-only modes against unauthorized manipulation of the encrypted data."XTS is supported by BestCrypt, Botan, NetBSD's cgd,[13] dm-crypt, FreeOTFE, TrueCrypt, VeraCrypt,[14] DiskCryptor, FreeBSD's geli, OpenBSD softraid disk encryption software, OpenSSL, Mac OS X Lion's FileVault 2, Windows 10's BitLocker[15] and wolfCrypt.XTS weaknesses[edit]XTS mode is susceptible to data manipulation and tampering, and applications must employ measures to detect modifications of data if manipulation and tampering is a concern: "...since there are no authentication tags then any ciphertext (original or modified by attacker) will be decrypted as some plaintext and there is no built-in mechanism to detect alterations. The best that can be done is to ensure that any alteration of the ciphertext will completely randomize the plaintext, and rely on the application that uses this transform to include sufficient redundancy in its plaintext to detect and discard such random plaintexts." This would require maintaining checksums for all data and metadata on disk, as done in ZFS or Btrfs. However, in commonly used file systems such as ext4 and NTFS only metadata is protected against tampering, while the detection of data tampering is non-existent.[16]The mode is susceptible to traffic analysis, replay and randomization attacks on sectors and 16-byte blocks. As a given sector is rewritten, attackers can collect fine-grained (16 byte) ciphertexts, which can be used for analysis or replay attacks (at a 16-byte granularity). It would be possible to define sector-wide block ciphers, unfortunately with degraded performance (see below).[17]CBC–mask–CBC (CMC) and ECB–mask–ECB (EME)[edit]CMC and EME protect even against the minor leak mentioned above for LRW. Unfortunately, the price is a twofold degradation of performance: each block must be encrypted twice; many consider this to be too high a cost, since the same leak on a sector level is unavoidable anyway.CMC, introduced by Halevi and Rogaway, stands for CBC–mask–CBC: the whole sector encrypted in CBC mode (with ), the ciphertext is masked by xoring with , and re-encrypted in CBC mode starting from the last block. When the underlying block cipher is a strong pseudorandom permutation (PRP) then on the sector level the scheme is a tweakable PRP. One problem is that in order to decrypt  one must sequentially pass over all the data twice.In order to solve this problem, Halevi and Rogaway introduced a parallelizable variant called EME (ECB–mask–ECB). It works in the following way:the plaintexts are xored with , shifted by different amount to the left, and are encrypted: ;the mask is calculated: , where  and ;intermediate ciphertexts are masked:  for  and ;the final ciphertexts are calculated:  for .Note that unlike LRW and CMC there is only a single key .CMC and EME were considered for standardization by SISWG. EME is patented, and so is not favored to be a primary supported mode.[18]Patents[edit]While the authenticated encryption scheme IAPM provides encryption as well as an authentication tag, the encryption component of the IAPM mode completely describes the LRW and XEX schemes above, and hence XTS without the ciphertext stealing aspect. This is described in detail in Figures 8 and 5 of the US patent 6,963,976.[19]See also[edit]Data remanenceCold boot attackDisk encryption softwareDisk encryption hardwareIEEE P1619, standardization project for encryption of the storage dataReferences[edit]1.^ Clemens Fruhwirth (July 18, 2005). "New Methods in Hard Disk Encryption" (PDF). Institute for Computer Languages: Theory and Logic Group (PDF). Vienna University of Technology.2.^ "Encrypting Virtual Memory" (Postscript).3.^ Milan Broz. "DMCrypt dm-crypt: Linux kernel device-mapper crypto target". gitlab.com. Retrieved April 5, 2015.4.^ Jakob Lell (2013-12-22). "Practical malleability attack against CBC-encrypted LUKS partitions".5.^ Latest SISWG and IEEE P1619 drafts and meeting information are on the P1619 home page [1].6.^ M. Liskov, R. Rivest, and D. Wagner. Tweakable block ciphers [2], CRYPTO '02 (LNCS, volume 2442), 2002.7.^ Jump up to:a b c Rogaway, Phillip (2004-09-24). "Efficient Instantiations of Tweakable Blockciphers and Refinements to Modes OCB and PMAC" (PDF). Dept. Of Computer Science(PDF). University of California, Davis.8.^ https://link.springer.com/content/pdf/10.1007/978-3-540-74462-7_8.pdf section 4.1.9.^ Karen McCabe (19 December 2007). "IEEE Approves Standards for Data Encryption". IEEE Standards Association. Archived from the original on 2008-03-06.10.^ Standard for Cryptographic Protection of Data on Block-Oriented Storage Devices. IEEE Xplore Digital Library. April 18, 2008. doi:10.1109/IEEESTD.2008.4493450. ISBN 978-0-7381-5363-6.11.^ Liskov, Moses; Minematsu, Kazuhiko (2008-09-02). "Comments on XTS-AES" (PDF)., On the Use of Two Keys, pp. 1–3.12.^ Morris Dworkin (January 2010). "Recommendation for Block Cipher Modes of Operation: The XTS-AES Mode for Confidentiality on Storage Devices" (PDF). NIST Special Publication 800-38E. National Institute of Standards and Technology.13.^ "NetBSD cryptographic disk driver".14.^ "Modes of Operation". VeraCrypt Documentation. IDRIX. Retrieved 2017-10-13.15.^ "What's new in BitLocker?". November 12, 2015. Retrieved 2015-11-15.16.^ Standard for Cryptographic Protection of Data on Block-Oriented Storage Devices (PDF), IEEE P1619/D16, 2007, p. 34, archived from the original (PDF) on 14 April 2016, retrieved 14 September 201217.^ Thomas Ptacek; Erin Ptacek (2014-04-30). "You Don't Want XTS".18.^ P. Rogaway, Block cipher mode of operation for constructing a wide-blocksize block cipher from a conventional block cipher, US Patent Application 20040131182 A1.19.^ * U.S. Patent 6,963,976, "Symmetric Key Authenticated Encryption Schemes" (filed Nov. 2000, issued Nov. 2005, expires 25 Nov. 2022) 3.Further reading[edit]S. Halevi and P. Rogaway, A Tweakable Enciphering Mode, CRYPTO '03 (LNCS, volume 2729), 2003.S. Halevi and P. Rogaway, A Parallelizable Enciphering Mode [5], 2003.Standard Architecture for Encrypted Shared Storage Media, IEEE Project 1619 (P1619), [6].SISWG, Draft Proposal for Key Backup Format [7], 2004.SISWG, Draft Proposal for Tweakable Wide-block Encryption [8], 2004.James Hughes, Encrypted Storage — Challenges and Methods [9]J. Alex Halderman, Seth D. Schoen, Nadia Heninger, William Clarkson, William Paul, Joseph A. Calandrino, Ariel J. Feldman, Jacob Appelbaum, and Edward W. Felten (2008-02-21). "Lest We Remember: Cold Boot Attacks on Encryption Keys" (PDF). Princeton University. Archived from the original (PDF) on 2008-05-14.Niels Fergusson (August 2006). "AES-CBC + Elephant Diffuser: A Disk Encryption Algorithm for Windows Vista" (PDF). Microsoft.External links[edit]Security in Storage Working Group SISWG."The eSTREAM project". Retrieved 2010-03-28.

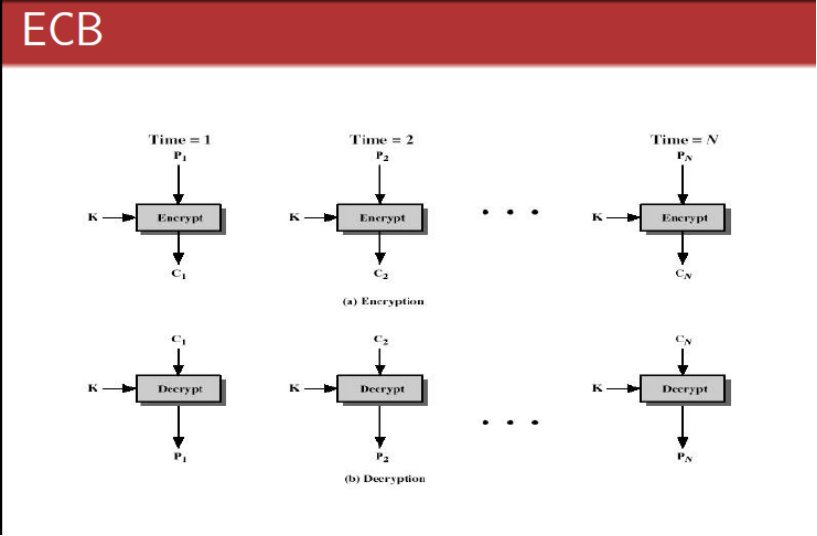
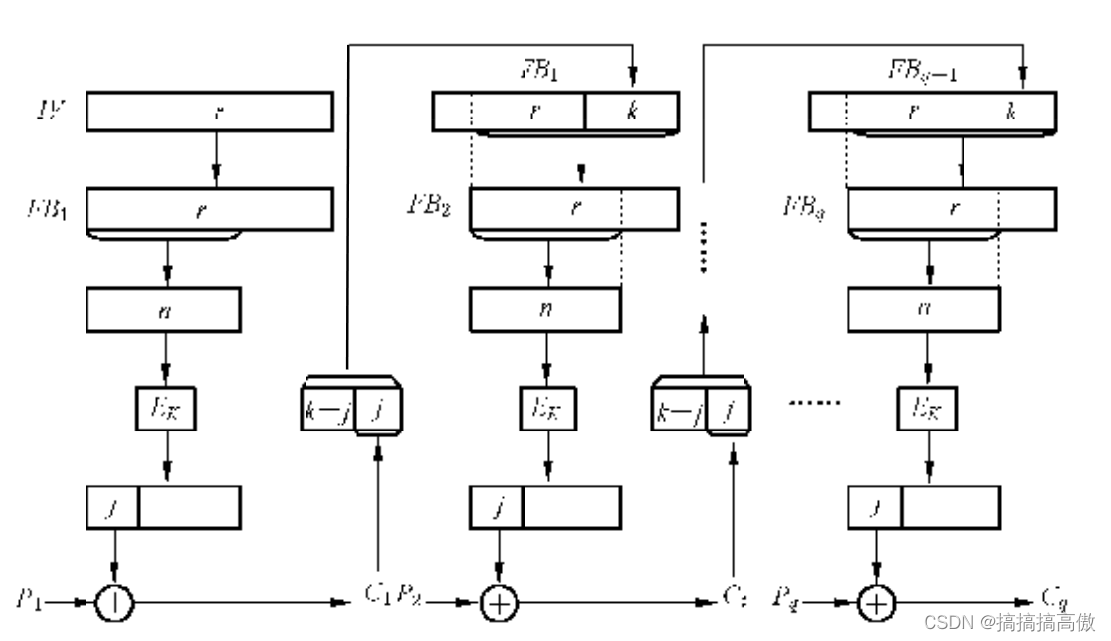
五种加解密模式（CBC、ECB、CTR、OCF、CFB） 分组密码有五种工作体制：1.电码本模式（Electronic Codebook Book (ECB)）；2.密码分组链接模式（Cipher Block Chaining (CBC)）；3.计算器模式（Counter (CTR)）；4.密码反馈模式（Cipher FeedBack (CFB)）；5.输出反馈模式（Output FeedBack (OFB)）。以下逐一介绍一下：1.电码本模式（Electronic Codebook Book (ECB)    这种模式是将整个明文分成若干段相同的小段，然后对每一小段进行加密。 2.密码分组链接模式（Cipher Block Chaining (CBC)）    这种模式是先将明文切分成若干小段，然后每一小段与初始块或者上一段的密文段进行异或运算后，再与密钥进行加密。 3.计算器模式（Counter (CTR)）        计算器模式不常见，在CTR模式中， 有一个自增的算子，这个算子用密钥加密之后的输出和明文异或的结果得到密文，相当于一次一密。这种加密方式简单快速，安全可靠，而且可以并行加密，但是在计算器不能维持很长的情况下，密钥只能使用一次。CTR的示意图如下所示：  4.密码反馈模式（Cipher FeedBack (CFB)）    这种模式较复杂。  5.输出反馈模式（Output FeedBack (OFB)）    这种模式较复杂。 以下附上C++源代码：/** *@autho stardust *@time 2013-10-10 *@param 实现AES五种加密模式的测试*/ #include <iostream>using namespace std; //加密编码过程函数,16位1和0int dataLen = 16; //需要加密数据的长度int encLen = 4; //加密分段的长度int encTable[4] = {1,0,1,0}; //置换表int data[16] = {1,0,0,1,0,0,0,1,1,1,1,1,0,0,0,0}; //明文int ciphertext[16]; //密文 //切片加密函数void encode(int arr[]) { for(int i=0;i<encLen;i++) { arr[i] = arr[i] ^ encTable[i]; } } //电码本模式加密，4位分段void ECB(int arr[]) { //数据明文切片 int a[4][4]; int dataCount = 0; //位置变量 for(int k=0;k<4;k++) { for(int t=0;t<4;t++) { a[k][t] = data[dataCount]; dataCount++; } } dataCount = 0;//重置位置变量 for(int i=0;i<dataLen;i=i+encLen) { int r = i/encLen;//行 int l = 0;//列 int encQue[4]; //编码片段 for(int j=0;j<encLen;j++) { encQue[j] = a[r][l]; l++; } encode(encQue); //切片加密 //添加到密文表中 for(int p=0;p<encLen;p++) { ciphertext[dataCount] = encQue[p]; dataCount++; } } cout<<"ECB加密的密文为："<<endl; for(int t1=0;t1<dataLen;t1++) //输出密文 { if(t1!=0 && t1%4==0) cout<<endl; cout<<ciphertext[t1]<<" "; } cout<<endl; cout<<"---------------------------------------------"<<endl; } //CBC//密码分组链接模式，4位分段void CCB(int arr[]) { //数据明文切片 int a[4][4]; int dataCount = 0; //位置变量 for(int k=0;k<4;k++) { for(int t=0;t<4;t++) { a[k][t] = data[dataCount]; dataCount++; } } dataCount = 0;//重置位置变量 int init[4] = {1,1,0,0}; //初始异或运算输入 //初始异或运算 for(int i=0;i<dataLen;i=i+encLen) { int r = i/encLen;//行 int l = 0;//列 int encQue[4]; //编码片段 //初始化异或运算 for(int k=0;k<encLen;k++) { a[r][k] = a[r][k] ^ init[k]; } //与Key加密的单切片 for(int j=0;j<encLen;j++) { encQue[j] = a[r][j]; } encode(encQue); //切片加密 //添加到密文表中 for(int p=0;p<encLen;p++) { ciphertext[dataCount] = encQue[p]; dataCount++; } //变换初始输入 for(int t=0;t<encLen;t++) { init[t] = encQue[t]; } } cout<<"CCB加密的密文为："<<endl; for(int t1=0;t1<dataLen;t1++) //输出密文 { if(t1!=0 && t1%4==0) cout<<endl; cout<<ciphertext[t1]<<" "; } cout<<endl; cout<<"---------------------------------------------"<<endl; } //CTR//计算器模式，4位分段void CTR(int arr[]) { //数据明文切片 int a[4][4]; int dataCount = 0; //位置变量 for(int k=0;k<4;k++) { for(int t=0;t<4;t++) { a[k][t] = data[dataCount]; dataCount++; } } dataCount = 0;//重置位置变量 int init[4][4] = {{1,0,0,0},{0,0,0,1},{0,0,1,0},{0,1,0,0}}; //算子表 int l = 0; //明文切片表列 //初始异或运算 for(int i=0;i<dataLen;i=i+encLen) { int r = i/encLen;//行 int encQue[4]; //编码片段 //将算子切片 for(int t=0;t<encLen;t++) { encQue[t] = init[r][t]; } encode(encQue); //算子与key加密 //最后的异或运算 for(int k=0;k<encLen;k++) { encQue[k] = encQue[k] ^ a[l][k]; } l++; //添加到密文表中 for(int p=0;p<encLen;p++) { ciphertext[dataCount] = encQue[p]; dataCount++; } } cout<<"CTR加密的密文为："<<endl; for(int t1=0;t1<dataLen;t1++) //输出密文 { if(t1!=0 && t1%4==0) cout<<endl; cout<<ciphertext[t1]<<" "; } cout<<endl; cout<<"---------------------------------------------"<<endl; } //CFB//密码反馈模式，4位分段void CFB(int arr[]) { //数据明文切片,切成2 * 8 片 int a[8][2]; int dataCount = 0; //位置变量 for(int k=0;k<8;k++) { for(int t=0;t<2;t++) { a[k][t] = data[dataCount]; dataCount++; } } dataCount = 0; //恢复初始化设置 int lv[4] = {1,0,1,1}; //初始设置的位移变量 int encQue[2]; //K的高两位 int k[4]; //K for(int i=0;i<2 * encLen;i++) //外层加密循环 { //产生K for(int vk=0;vk<encLen;vk++) { k[vk] = lv[vk]; } encode(k); for(int k2=0;k2<2;k2++) { encQue[k2] = k[k2]; } //K与数据明文异或产生密文 for(int j=0;j<2;j++) { ciphertext[dataCount] = a[dataCount/2][j] ^ encQue[j]; dataCount++; } //lv左移变换 lv[0] = lv[2]; lv[1] = lv[3]; lv[2] = ciphertext[dataCount-2]; lv[3] = ciphertext[dataCount-1]; } cout<<"CFB加密的密文为："<<endl; for(int t1=0;t1<dataLen;t1++) //输出密文 { if(t1!=0 && t1%4==0) cout<<endl; cout<<ciphertext[t1]<<" "; } cout<<endl; cout<<"---------------------------------------------"<<endl; } //OFB//输出反馈模式，4位分段void OFB(int arr[]) { //数据明文切片,切成2 * 8 片 int a[8][2]; int dataCount = 0; //位置变量 for(int k=0;k<8;k++) { for(int t=0;t<2;t++) { a[k][t] = data[dataCount]; dataCount++; } } dataCount = 0; //恢复初始化设置 int lv[4] = {1,0,1,1}; //初始设置的位移变量 int encQue[2]; //K的高两位 int k[4]; //K for(int i=0;i<2 * encLen;i++) //外层加密循环 { //产生K for(int vk=0;vk<encLen;vk++) { k[vk] = lv[vk]; } encode(k); for(int k2=0;k2<2;k2++) { encQue[k2] = k[k2]; } //K与数据明文异或产生密文 for(int j=0;j<2;j++) { ciphertext[dataCount] = a[dataCount/2][j] ^ encQue[j]; dataCount++; } //lv左移变换 lv[0] = lv[2]; lv[1] = lv[3]; lv[2] = encQue[0]; lv[3] = encQue[1]; } cout<<"CFB加密的密文为："<<endl; for(int t1=0;t1<dataLen;t1++) //输出密文 { if(t1!=0 && t1%4==0) cout<<endl; cout<<ciphertext[t1]<<" "; } cout<<endl; cout<<"---------------------------------------------"<<endl; } void printData() { cout<<"以下示范AES五种加密模式的测试结果："<<endl; cout<<"---------------------------------------------"<<endl; cout<<"明文为："<<endl; for(int t1=0;t1<dataLen;t1++) //输出密文 { if(t1!=0 && t1%4==0) cout<<endl; cout<<data[t1]<<" "; } cout<<endl; cout<<"---------------------------------------------"<<endl; }int main() { printData(); ECB(data); CCB(data); CTR(data); CFB(data); OFB(data); return 0; }

分组密码算法的工作模式——KeyWrap密钥封装模式 密钥封装是为了对密钥进行保护，比如密钥存储在不太安全的存储设备中，或者密钥需要在网络中传输。早在2001年，NIST就发布了AES Key Wrap Specification。2002年，IETF在RFC 3394中也描述了密钥封装算法AES-KeyWrap Algorithm，电信行业协会发布了使用TDES的密钥封装算法。2008年，美国标准认可委员会（Accredited Standards Committee X9, Inc.）发布了金融服务业的密钥封装算法。2009年，RFC 5649 描述了带填充的密钥封装算法。 2012年，NIST SP 800-38F描述了AES KW、AES KWP（带填充的密钥封装算法）和TDES的TKW。NIST的这三个算法和RFC等的描述几乎完全一致。     以下描述以NIST SP 800-38F为主，结合RFC 3394和RFC 5649。     参考文献Key Wrap - Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/Key_WrapNIST Special Publication 800-38F: Recommendation for Block Cipher Modes of Operation Methods for Key Wrapping, December 2012.J. Schaad and R. Housley, Advanced Encryption Standard (AES) Key Wrap Algorithm, RFC 3394, September, 2002.R. Housley and M. Dworkin, Advanced Encryption Standard (AES) Key Wrap with Padding Algorithm, RFC 5649, August, 2009.ANSI/TIA-102.AACA-1-2002: Project 25 – Digital Radio Over-the-Air-Rekeying (OTAR) Protocol: Addendum 1 – Key Management Security Requirements for Type 3 Block Encryption Algorithms, Telecommunications Industry Association, November, 2002.ANS X9.102-2008, Symmetric Key Cryptography For the Financial Services Industry—Wrapping of Keys and Associated Data, Accredited Standards Committee X9, Inc., June, 2008. 密钥封装有三种KW          基于AES的密钥封装，不使用填充。KWP   基于AES的密钥封装，使用填充。TKW   基于TDES的密钥封装，不使用填充。 算法明文密文使用模块KW2—254-1个64bit长3—254个64bit长W和W-1KWP1—232-1个8bit长2—232个8bit长W和W-1TKW2—228-1个32bit长3—228个32bit长TW和TW-1WC = W(S)模块准备：K(即KEK)128-bit 分组密码CIPH.输入：S，长度为n×64bit，n ≥ 3.输出C，与S等长（长度为n×64bit，n ≥ 3）。步骤初始化s = 6(n-1).S=S1 || S2 ||… || Sn . Si都是64itA0 = S1.For i = 2, …, nR0i = Si.迭代For t = 1, …, s          At = MSB64(CIPHK(At-1 || R2t-1)) ⊕ [t]64;          For i = 2, …, n-1:Rit = Ri+1t-1;          Rnt = LSB64(CIPHK (At-1 || R2t-1)).输出结果C1 = As.For i = 2, …, nCi = Ris.Return C1 || C2 || … || Cn. W的示意图如下W的示意图 W中迭代器的示意图如下：W中迭代器的示意图 W-1S = W-1(C)模块准备：K(即KEK)128-bit 分组密码CIPH的逆函数CIPH-1输入：C，长度为n×64bit，n ≥ 3.输出S，与c等长（长度为n×64bit，n ≥ 3）。步骤初始化s = 6(n-1).C = C1 || C2 ||… || Cn . Ci都是64bitAs = C1.For i = 2, …, nRsi = Ci.迭代For t = s, …, 1          At-1 = MSB64((CIPH-1K(At ⊕[t]64)) || Rnt);R2t-1 = LSB64(CIPH-1K ((At ⊕[t]64) || Rnt).          For i = 2, …, n-1:Ri+1t-1 = Rit ; 输出结果S1 = A0.For i = 2, …, nSi = Ri0.Return S1 || S2 || … || Sn. KWKW的加密KW-AE(P)和解密KW-AD(C)。加密C = KW-AE(P)输入：明文P输出：密文CICV1 = 0xA6A6A6A6A6A6A6A6.S = ICV1 || P.Return C = W(S). 解密P = KW-AD(C)输入：密文C输出：明文P或者失败ICV1 = 0xA6A6A6A6A6A6A6A6.S = W-1(C).If MSB64(S) ≠ICV1, return FAIL and stop.Return P = LSB64(n-1)(S). RFC 3394对KW采用一种便于软件实现的描述方式。输入:明文 P = P1||P2||...||Pn，n个64-bit密钥 K (KEK).输出:密文 C = C0||C1||...||Cn,(n+1)个64-bit步骤1)  A = IV, IV = 0xA6A6A6A6A6A6A6A6    For i = 1 to n, R[i] = P[i]2)  For j = 0 to 5 {        For i=1 to n {            B = AES(K, A || R[i])            A = MSB(64, B) ⊕ t,其中t = (n*j)+i            R[i] = LSB(64, B)        }//i    }//j3)  C[0] = AFor i = 1 to n, C[i] = R[i]Return C = C[0] || C[1] || ... || C[n]KWP带填充的KW加密KWP-AE(P)和带填充的KW解密KWP-AD(C)。加密C = KWP-AE(P)输入：明文P输出：密文CICV2 = 0xA65959A6.2. PAD = 08×padlenS = ICV2 || [len(P)/8]32 || P || PAD5.  If len(P) ≤ 64,   return C = CIPHK(S);else,            return C = W(S). 这里的padlen是指将明文P填充为64bit的整数倍时需要填充（填充数据为全零字节）的最短字节数，可以为0。消息S表示在填充后消息的前面再加64比特的特殊消息，以保证S长度最少为一个分组大小（128bit）。如果S长度只有一个分组大小，则直接执行AES。 解密P = KW-AD(C)输入：密文C，C = C1||C2||...||Cn, n个64-bit输出：明文P或者失败1.  ICV2 = 0xA65959A6.If n = 2, S = CIPH-1K(C); if n > 2, S = W-1(C).If MSB32(S) ≠ ICV2, return FAIL and stop.4.  Plen = int(LSB32(MSB64(S))).padlen = 8(n-1)-Plen.If padlen < 0 or padlen > 7, return FAIL and stop.If LSB8×padlen(S) ≠ 08×padlen, return FAIL and stop.Return P = MSB8×Plen(LSB64×(n-1)(S)).TKW这个和KW其实是一样的，只有一下几个地方有区别：使用的密码算法不一样：KW采用AES；TKW采用TDES分组大小不一样导致半分组大小不一样：KW半分组大小64bit；TKW半分组大小32bit。详细流程可辅助参见KW。注意：TKW没有加填充的所谓TKWP算法。测试数据NIST SP 800-38F里面没有测试数据；测试数据可以在RFC 3394和RFC 5649里面查。LibTomCrypt目前尚不支持KeyWrap。————————————————版权声明：本文为CSDN博主「网糸隹」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。原文链接：https://blog.csdn.net/samsho2/article/details/85263837

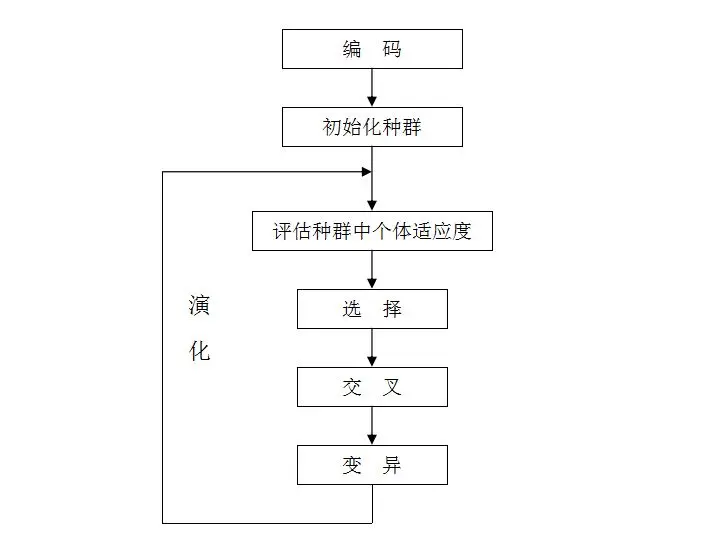
什么是遗传算法 01 什么是遗传算法？1.1 遗传算法的科学定义遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择、交叉和变异构成了遗传算法的遗传操作；参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。1.2 遗传算法的执行过程(参照百度百科)遗传算法是从代表问题可能潜在的解集的一个种群（population）开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往进行简化，如二进制编码。初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代（generation）演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度（fitness）大小选择（selection）个体，并借助于自然遗传学的遗传算子（genetic operators）进行组合交叉（crossover）和变异（mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码（decoding），可以作为问题近似最优解。1.3 遗传算法过程图解02 相关生物学术语为了大家更好了解遗传算法，在此之前先简单介绍一下相关生物学术语，大家了解一下即可。基因型(genotype)：性状染色体的内部表现；表现型(phenotype)：染色体决定的性状的外部表现，或者说，根据基因型形成的个体的外部表现；进化(evolution)：种群逐渐适应生存环境，品质不断得到改良。生物的进化是以种群的形式进行的。适应度(fitness)：度量某个物种对于生存环境的适应程度。选择(selection)：以一定的概率从种群中选择若干个个体。一般，选择过程是一种基于适应度的优胜劣汰的过程。复制(reproduction)：细胞分裂时，遗传物质DNA通过复制而转移到新产生的细胞中，新细胞就继承了旧细胞的基因。交叉(crossover)：两个染色体的某一相同位置处DNA被切断，前后两串分别交叉组合形成两个新的染色体。也称基因重组或杂交；变异(mutation)：复制时可能（很小的概率）产生某些复制差错，变异产生新的染色体，表现出新的性状。编码(coding)：DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。解码(decoding)：基因型到表现型的映射。个体（individual）：指染色体带有特征的实体；种群（population）：个体的集合，该集合内个体数称为种群03 问题引出与解决3.1 一元函数最大值问题如下的函数图像：现在我们要在既定的区间内找出函数的最大值。学过高中数学的孩纸都知道，上面的函数存在着很多的极大值和极小值。而最大值则是指定区间的极大值中的最大的那一个。从图像上具体表现为，极大值像是一座座山峰，极小值则是像一座座山谷。因此，我们也可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。这些山峰对应着局部最优解，其中有一个山峰是海拔最高的，这个山峰则对应的是全局最优解。那么，遗传算法要做的就是尽量爬到最高峰，而不是困在较低的小山峰上。（如果问题求解是最小值，那么要做的就是尽量走到最低谷，道理是一样的）。3.2 "袋鼠蹦跳"既然我们把函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们可以设想所得到的每一个解就是一只袋鼠，我们希望它们不断的向着更高处跳去，直到跳到最高的山峰。所以求最大值的过程就转化成一个“袋鼠跳”的过程。下面介绍介绍“袋鼠跳”的几种方式。爬山算法：一只袋鼠朝着比现在高的地方跳去。它找到了不远处的最高的山峰。但是这座山不一定是最高峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。模拟退火：袋鼠喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高峰跳去。这就是模拟退火算法。遗传算法：有很多袋鼠，它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年，就在一些海拔高度较低的地方射杀一些袋鼠。于是，不断有袋鼠死于海拔较低的地方，而越是在海拔高的袋鼠越是能活得更久，也越有机会生儿育女。就这样经过许多年，这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上，可是在所有的袋鼠中，只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。04 大体实现过程遗传算法中每一条染色体，对应着遗传算法的一个解决方案，一般我们用适应性函数（fitness function）来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。遗传算法的实现过程实际上就像自然界的进化过程那样。下面我们用袋鼠跳中的步骤一一对应解释，以方便大家理解：首先寻找一种对问题潜在解进行“数字化”编码的方案。（建立表现型和基因型的映射关系）随机初始化一个种群（那么第一批袋鼠就被随意地分散在山脉上），种群里面的个体就是这些数字化的编码。接下来，通过适当的解码过程之后（得到袋鼠的位置坐标）。用适应性函数对每一个基因个体作一次适应度评估（袋鼠爬得越高当然就越好，所以适应度相应越高）。用选择函数按照某种规定择优选择（每隔一段时间，射杀一些所在海拔较低的袋鼠，以保证袋鼠总体数目持平。）。让个体基因变异（让袋鼠随机地跳一跳）。然后产生子代（希望存活下来的袋鼠是多产的，并在那里生儿育女）。遗传算法并不保证你能获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。（你不必去指导袋鼠向那边跳，跳多远。）而只要简单的“否定”一些表现不好的个体就行了。（把那些总是爱走下坡路的袋鼠射杀，这就是遗传算法的精粹！）由此我们可以得出遗传算法的一般步骤：1.随机产生种群。2.根据策略判断个体的适应度，是否符合优化准则，若符合，输出最佳个体及其最优解，结束。否则，进行下一步。3.依据适应度选择父母，适应度高的个体被选中的概率高，适应度低的个体被淘汰。4.用父母的染色体按照一定的方法进行交叉，生成子代。5.对子代染色体进行变异。由交叉和变异产生新一代种群，返回步骤2，直到最优解产生。具体图解可以回到1.3查看。05 开始我们的进化(具体实现细节)5.1 先从编码说起编码是应用遗传算法时要解决的首要问题，也是设计遗传算法时的一个关键步骤。编码方法影响到交叉算子、变异算子等遗传算子的运算方法，大很大程度上决定了遗传进化的效率。迄今为止人们已经提出了许多种不同的编码方法。总的来说，这些编码方法可以分为三大类：二进制编码法、浮点编码法、符号编码法。下面分别进行介绍：5.1.1 二进制编码法就像人类的基因有AGCT 4种碱基序列一样。不过在这里我们只用了0和1两种碱基,然后将他们串成一条链形成染色体。一个位能表示出2种状态的信息量，因此足够长的二进制染色体便能表示所有的特征。这便是二进制编码。如下：1110001010111它由二进制符号0和1所组成的二值符号集。它有以下一些优点：1.编码、解码操作简单易行2.交叉、变异等遗传操作便于实现3.合最小字符集编码原则4.利用模式定理对算法进行理论分析。二进制编码的缺点是：对于一些连续函数的优化问题，由于其随机性使得其局部搜索能力较差，如对于一些高精度的问题（如上题），当解迫近于最优解后，由于其变异后表现型变化很大，不连续，所以会远离最优解，达不到稳定。5.1.２ 浮点编码法二进制编码虽然简单直观，但明显地。但是存在着连续函数离散化时的映射误差。个体长度较短时，可能达不到精度要求，而个体编码长度较长时，虽然能提高精度，但增加了解码的难度，使遗传算法的搜索空间急剧扩大。所谓浮点法，是指个体的每个基因值用某一范围内的一个浮点数来表示。在浮点数编码方法中，必须保证基因值在给定的区间限制范围内，遗传算法中所使用的交叉、变异等遗传算子也必须保证其运算结果所产生的新个体的基因值也在这个区间限制范围内。如下所示：1.2-3.2-5.3-7.2-1.4-9.7浮点数编码方法有下面几个优点：1.适用于在遗传算法中表示范围较大的数2.适用于精度要求较高的遗传算法3.便于较大空间的遗传搜索4.改善了遗传算法的计算复杂性，提高了运算交率5.便于遗传算法与经典优化方法的混合使用6.便于设计针对问题的专门知识的知识型遗传算子7.便于处理复杂的决策变量约束条件5.1.3 符号编码法符号编码法是指个体染色体编码串中的基因值取自一个无数值含义、而只有代码含义的符号集如｛A,B,C…｝。符号编码的主要优点是：1.符合有意义积术块编码原则2.便于在遗传算法中利用所求解问题的专门知识3.便于遗传算法与相关近似算法之间的混合使用。5.2 为我们的袋鼠染色体编码在上面介绍了一系列编码方式以后，那么，如何利用上面的编码来为我们的袋鼠染色体编码呢？首先我们要明确一点：编码无非就是建立从基因型到表现型的映射关系。这里的表现型可以理解为个体特征（比如身高、体重、毛色等等）。那么，在此问题下，我们关心的个体特征就是：袋鼠的位置坐标（因为我们要把海拔低的袋鼠给杀掉）。无论袋鼠长什么样，爱吃什么。我们关心的始终是袋鼠在哪里，并且只要知道了袋鼠的位置坐标（位置坐标就是相应的染色体编码，可以通过解码得出），我们就可以：1.在喜马拉雅山脉的地图上找到相应的位置坐标，算出海拔高度。（相当于通过自变量求得适应函数的值）然后判读该不该射杀该袋鼠。2.可以知道染色体交叉和变异后袋鼠新的位置坐标。回到3.1中提的求一元函数最大值的问题。在上面我们把极大值比喻为山峰，那么，袋鼠的位置坐标可以比喻为区间[-1, 2]的某一个x坐标（有了x坐标，再通过函数表达式可以算出函数值 <==> 得到了袋鼠染色体编码，解码得到位置坐标，在喜马拉雅山脉地图查询位置坐标算出海拔高度）。这个x坐标是一个实数，现在，说白了就是怎么对这个x坐标进行编码。下面我们以二进制编码为例讲解，不过这种情况下以二进制编码比较复杂就是了。（如果以浮点数编码，其实就很简洁了，就一浮点数而已。）我们说过，一定长度的二进制编码序列，只能表示一定精度的浮点数。在这里假如我们要求解精确到六位小数，由于区间长度为2 - (-1) = 3 ,为了保证精度要求，至少把区间[-1,2]分为3 × 10^6等份。又因为2^21 = 2097152 < 3*10^6 < 2^22 = 4194304所以编码的二进制串至少需要22位。把一个二进制串(b0,b1,....bn)转化为区间里面对应的实数值可以通过下面两个步骤：1.将一个二进制串代表的二进制数转化为10进制数：对应区间内的实数：例如一个二进制串(1000101110110101000111)2通过上面换算以后，表示实数值0.637197。好了，上面的编码方式只是举个例子让大家更好理解而已，编码的方式千奇百怪，层出不穷，每个问题可能采用的编码方式都不一样。在这一点上大家要注意。5.3 评价个体的适应度--适应度函数（fitness function）前面说了，适应度函数主要是通过个体特征从而判断个体的适应度。在本例的袋鼠跳中，我们只关心袋鼠的海拔高度，以此来判断是否该射杀该袋鼠。这样一来，该函数就非常简单了。只要输入袋鼠的位置坐标，在通过相应查找运算，返回袋鼠当前位置的海拔高度就行。适应度函数也称评价函数，是根据目标函数确定的用于区分群体中个体好坏的标准。适应度函数总是非负的，而目标函数可能有正有负，故需要在目标函数与适应度函数之间进行变换。评价个体适应度的一般过程为：对个体编码串进行解码处理后，可得到个体的表现型。由个体的表现型可计算出对应个体的目标函数值。根据最优化问题的类型，由目标函数值按一定的转换规则求出个体的适应度。5.4 射杀一些袋鼠--选择函数（selection）遗传算法中的选择操作就是用来确定如何从父代群体中按某种方法选取那些个体，以便遗传到下一代群体。选择操作用来确定重组或交叉个体，以及被选个体将产生多少个子代个体。前面说了，我们希望海拔高的袋鼠存活下来，并尽可能繁衍更多的后代。但我们都知道，在自然界中，适应度高的袋鼠越能繁衍后代，但这也是从概率上说的而已。毕竟有些适应度低的袋鼠也可能逃过我们的眼睛。那么，怎么建立这种概率关系呢？下面介绍几种常用的选择算子：轮盘赌选择（Roulette Wheel Selection）：是一种回放式随机采样方法。每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值和的比例。选择误差较大。随机竞争选择（Stochastic Tournament）：每次按轮盘赌选择一对个体，然后让这两个个体进行竞争，适应度高的被选中，如此反复，直到选满为止。最佳保留选择：首先按轮盘赌选择方法执行遗传算法的选择操作，然后将当前群体中适应度最高的个体结构完整地复制到下一代群体中。无回放随机选择（也叫期望值选择Excepted Value Selection）：根据每个个体在下一代群体中的生存期望来进行随机选择运算。方法如下:（1） 计算群体中每个个体在下一代群体中的生存期望数目N。（2） 若某一个体被选中参与交叉运算，则它在下一代中的生存期望数目减去0.5，若某一个体未 被选中参与交叉运算，则它在下一代中的生存期望数目减去1.0。（3） 随着选择过程的进行，若某一个体的生存期望数目小于0时，则该个体就不再有机会被选中。确定式选择：按照一种确定的方式来进行选择操作。具体操作过程如下：（1） 计算群体中各个个体在下一代群体中的期望生存数目N。（2） 用N的整数部分确定各个对应个体在下一代群体中的生存数目。（3） 用N的小数部分对个体进行降序排列，顺序取前M个个体加入到下一代群体中。至此可完全确定出下一代群体中Ｍ个个体。无回放余数随机选择：可确保适应度比平均适应度大的一些个体能够被遗传到下一代群体中，因而选择误差比较小。均匀排序：对群体中的所有个体按期适应度大小进行排序，基于这个排序来分配各个个体被选中的概率。最佳保存策略：当前群体中适应度最高的个体不参与交叉运算和变异运算，而是用它来代替掉本代群体中经过交叉、变异等操作后所产生的适应度最低的个体。随机联赛选择：每次选取几个个体中适应度最高的一个个体遗传到下一代群体中。排挤选择：新生成的子代将代替或排挤相似的旧父代个体，提高群体的多样性。下面以轮盘赌选择为例给大家讲解一下：假如有５条染色体，他们的适应度分别为５、８、３、７、２。那么总的适应度为：F = 5 + 8 + 3 + 7 + 2 = 25。那么各个个体的被选中的概率为：α1 = ( 5 / 25 ) * 100% = 20%α2 = ( 8 / 25 ) * 100% = 32%α3 = ( 3 / 25 ) * 100% = 12%α4 = ( 7 / 25 ) * 100% = 28%α5 = ( 2 / 25 ) * 100% = 8%所以转盘如下：当指针在这个转盘上转动，停止下来时指向的个体就是天选之人啦。可以看出，适应性越高的个体被选中的概率就越大。5.５ 遗传--染色体交叉(crossover)遗传算法的交叉操作，是指对两个相互配对的染色体按某种方式相互交换其部分基因，从而形成两个新的个体。适用于二进制编码个体或浮点数编码个体的交叉算子：单点交叉（One-point Crossover）：指在个体编码串中只随机设置一个交叉点，然后再该点相互交换两个配对个体的部分染色体。两点交叉与多点交叉：(1) 两点交叉（Two-point Crossover）：在个体编码串中随机设置了两个交叉点，然后再进行部分基因交换。5(2) 多点交叉（Multi-point Crossover）均匀交叉（也称一致交叉，Uniform Crossover）：两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换，从而形成两个新个体。算术交叉（Arithmetic Crossover）：由两个个体的线性组合而产生出两个新的个体。该操作对象一般是由浮点数编码表示的个体。10.咳咳，根据国际惯例。还是抓一个最简单的二进制单点交叉为例来给大家讲解讲解。二进制编码的染色体交叉过程非常类似高中生物中所讲的同源染色体的联会过程――随机把其中几个位于同一位置的编码进行交换，产生新的个体。对应的二进制交叉：5.6 变异--基因突变(Mutation)遗传算法中的变异运算，是指将个体染色体编码串中的某些基因座上的基因值用该基因座上的其它等位基因来替换，从而形成新的个体。例如下面这串二进制编码：101101001011001经过基因突变后，可能变成以下这串新的编码：001101011011001以下变异算子适用于二进制编码和浮点数编码的个体：基本位变异（Simple Mutation）：对个体编码串中以变异概率、随机指定的某一位或某几位仅因座上的值做变异运算。均匀变异（Uniform Mutation）：分别用符合某一范围内均匀分布的随机数，以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。（特别适用于在算法的初级运行阶段）边界变异（Boundary Mutation）：随机的取基因座上的两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。非均匀变异：对原有的基因值做一随机扰动，以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后，相当于整个解向量在解空间中作了一次轻微的变动。高斯近似变异：进行变异操作时用符号均值为Ｐ的平均值，方差为P**2的正态分布的一个随机数来替换原有的基因值。06 代码实现环节好了，上面我们介绍了一大截具体原理。现在就是把各个具体的零部件组装起来，动手写我们的代码了。欲获取代码，请关注我们的微信公众号【程序猿声】，在后台回复：GA代码。即可获取。作者：番茄鸡蛋炒饭被抢注啦链接：https://www.jianshu.com/p/ae5157c26af9来源：简书著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。