搜索到
17
篇与
的结果
-
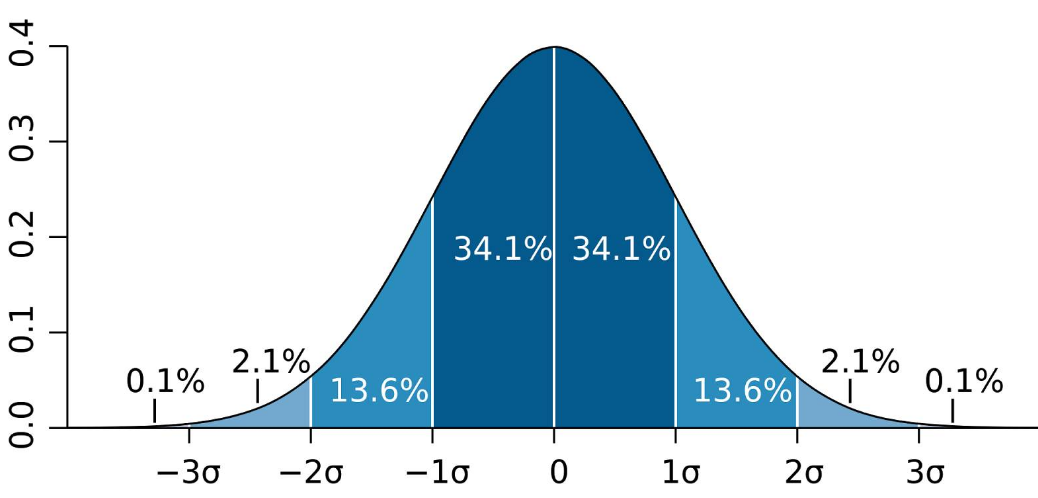
 一份数学小白也能读懂的「马尔可夫链蒙特卡洛方法」入门指南 机器之心2017年12月24日12:46作者:Ben Shaver机器之心编译参与:黄小天、刘晓坤在众多经典的贝叶斯方法中,马尔可夫链蒙特卡洛(MCMC)由于包含大量数学知识,且计算量很大,而显得格外特别。本文反其道而行之,试图通过通俗易懂且不包含数学语言的方法,帮助读者对 MCMC 有一个直观的理解,使得毫无数学基础的人搞明白 MCMC。在我们中的很多人看来,贝叶斯统计学家不是巫术师,就是完全主观的胡说八道者。在贝叶斯经典方法中,马尔可夫链蒙特卡洛(Markov chain Monte Carlo/MCMC)尤其神秘,其中数学很多,计算量很大,但其背后原理与数据科学有诸多相似之处,并可阐释清楚,使得毫无数学基础的人搞明白 MCMC。这正是本文的目标。那么,到底什么是 MCMC 方法?一言以蔽之:MCMC 通过在概率空间中随机采样以近似兴趣参数(parameter of interest)的后验分布。我将在本文中做出简短明了的解释,并且不借助任何数学知识。首先,解释重要的术语。「兴趣参数」(parameter of interest)可以总结我们感兴趣现象的一些数字。我们通常使用统计学评估参数,比如,如果想要了解成年人的身高,我们的兴趣参数可以是精确到英寸的平均身高。「分布」是参数的每个可能值、以及我们有多大可能观察每个参数的数学表征,其最著名的实例是钟形曲线:在贝叶斯统计学中,分布还有另外一种解释。贝叶斯不是仅仅表征一个参数值以及每个参数有多大可能是真值,而是把分布看作是我们对参数的「信念」。因此,钟形曲线表明我们非常确定参数值相当接近于零,但是我们认为在一定程度上真值高于或低于该值的可能性是相等的。事实上,人的身高确实遵从一个正态曲线,因此我们假定平均身高的真值符合钟形曲线,如下所示:很明显,上图表征是巨人的身高分布,因为据图可知,最有可能的平均身高是 6'2"(但他们也并非超级自信)。让我们假设其中某个人后来收集到一些数据,并且观察了身高在 5"和 6"之间的一些人。我们可以用另一条正态曲线表征下面的数据,该曲线表明了哪些平均身高值能最好地解释这些数据:在贝叶斯统计中,表征我们对参数信念的分布被称为「先验分布」,因为它在我们看到任何数据之前捕捉到了我们的信念。「可能性分布」(likelihood distribution)通过表征一系列参数值以及伴随的每个参数值解释观察数据的可能性,以总结数据之中的信息。评估最大化可能性分布的参数值只是回答这一问题:什么参数值会使我们更可能观察到已经观察过的数据?如果没有先验信念,我们可能无法对此作出评估。但是,贝叶斯分析的关键是结合先验与可能性分布以确定后验分布。它可以告诉我们哪个参数值最大化了观察到已观察过的特定数据的概率,并把先验信念考虑在内。在我们的实例中,后验分布如下所示:如上所示,红线表征后验分布。你可以将其看作先验和可能性分布的一种平均值。由于先验分布较小且更加分散,它表征了一组关于平均身高真值的「不太确定」的信念。同时,可能性分布在相对较窄的范围内总结数据,因此它表征了对真参数值的「更确定」的猜测。当先验与可能性分布结合在一起,数据(由可能性分布表征)主导了假定存在于这些巨人之中的个体的先验弱信念。尽管该个体依然认为平均身高比数据告诉他的稍高一些,但是他非常可能被数据说服。在两条钟形曲线的情况下,求解后验分布非常容易。有一个结合了两者的简单等式。但是如果我们的先验和可能性分布表现很差呢?有时使用非简化的形状建模数据或先验信念时是最精确的。如果可能性分布需要带有两个峰值的分布才能得到最好地表征呢?并且出于某些原因我们想要解释一些非常奇怪的先验分布?通过手动绘制一个丑陋的先验分布,我已可视化了该情景,如下所示:可视化由 Matplotlib 渲染,并使用 MS Paint 做了改善如前所述,存在一些后验分布,它给出了每个参数值的可能性分布。但是很难得到完整的分布,也无法解析地求解。这就是使用 MCMC 方法的时候了。MCMC 允许我们在无法直接计算的情况下评估后验分布的形状。为了理解其工作原理,我将首先介绍蒙特卡洛模拟(Monte Carlo simulation),接着讨论马尔可夫链。蒙特卡洛模拟只是一种通过不断地生成随机数来评估固定参数的方法。通过生成随机数并对其做一些计算,蒙特卡洛模拟给出了一个参数的近似值(其中直接计算是不可能的或者计算量过大)。假设我们想评估下图中的圆圈面积:由于圆在边长为 10 英寸的正方形之内,所以通过简单计算可知其面积为 78.5 平方英寸。但是,如果我们随机地在正方形之内放置 20 个点,接着我们计算点落在圆内的比例,并乘以正方形的面积,所得结果非常近似于圆圈面积。由于 15 个点落在了圆内,那么圆的面积可以近似地为 75 平方英寸,对于只有 20 个随机点的蒙特卡洛模拟来说,结果并不差。现在,假设我们想要计算下图中由蝙蝠侠方程(Batman Equation)绘制的图形的面积:我们从来没有学过一个方程可以求这样的面积。不管怎样,通过随机地放入随机点,蒙特卡洛模拟可以相当容易地为该面积提供一个近似值。蒙特卡洛模拟不只用于估算复杂形状的面积。通过生成大量随机数字,它还可用于建模非常复杂的过程。实际上,蒙特卡洛模拟还可以预测天气,或者评估选举获胜的概率。理解 MCMC 方法的第二个要素是马尔科夫链(Markov chains)。马尔科夫链由存在概率相关性的事件的序列构成。每个事件源于一个结果集合,根据一个固定的概率集合,每个结果决定了下一个将出现的结果。马尔科夫链的一个重要特征是「无记忆性」:可能需要用于预测下一个时间的一切都已经包含在当前的状态中,从事件的历史中得不到任何新信息。例如 Chutes and Ladders 这个游戏就展示了这种无记忆性,或者说马尔科夫性,但在现实世界中很少事物是这种性质的。尽管如此,马尔科夫链也是理解现实世界的强大工具。在十九世纪,人们观察到钟形曲线在自然中是一种很常见的模式。(我们注意到,例如,人类的身高服从钟形曲线分布。)Galton Boards 曾通过将弹珠坠落并通过布满木钉的板模拟了重复随机事件的平均值,在弹珠的最终数量分布中重现了钟形曲线:俄罗斯数学家和神学家 Pavel Nekrasov 认为钟形曲线,或者更一般的说,大数规律只不过是小孩子的游戏和普通的谜题中的伪假象,其中每个事件之间都是完全独立的。他认为现实世界中的互相依赖的事件,例如人类行为,并不遵循漂亮的数学模式或分布。Andrey Markov(马尔科夫链正是以他的名字命名)试图证明非独立的事件可能也遵循特定的模式。他的其中一个最著名的例子是从一份俄罗斯诗歌作品中数出几千个两字符对(two-character pairs)。他使用这些两字符对计算了每个字符的条件概率。即,给定一个确定的上述字母或空白,关于下一个字母将是 A、T 或者空白等,存在一个确定的概率。通过这些概率,Markov 可以模拟一个任意的长字符序列。这就是马尔科夫链。虽然早先的几个字符很大程度上依赖于初始字符的选择,Markov 表明在长字符序列中,字符的分布会出现特定的模式。因此,即使是互相依赖的事件,如果服从固定的概率分布,将遵循平均水平的模式。举一个更有意义的例子,假设你住在一个有 5 个房间的房子里,里面有一个卧室、浴室、客厅、厨房、饭厅。然后我们收集一些数据,假定只需要当前你所处的房间和相应的时间就可以预测下一个你所处的房间的概率。例如,如果你在厨房,你有 30% 的概率会留在厨房,有 30% 的概率会走到饭厅,有 20% 的概率会走到客厅,有 10% 的概率会走到浴室,以及有 10% 的概率会走到卧室。使用每个房间的概率集合,我们可以构建一个关于你接下来要去的房间的预测链。如果想预测一个人处于厨房之后所在的房间,基于几个状态而做出预测可能有效。但由于我们的预测仅仅基于一个人在房子中的单次观察,可以合理地认为预测结果是不够好的。例如,如果一个人从卧室走到浴室,相比从厨房走到浴室的情况,他更可能会返回原来的房间。因此,马尔科夫链并不真正适用于现实世界。然而,通过迭代运行马尔科夫链数千次,确实能给出关于你接下来可能所处的房间的长期预测。更重要的是,这个预测并不受这个人起始所处的房间的影响。对此可以直观地理解为:在模拟和描述长期过程(或普遍情况)一个人所处房间的概率时,时间因素是不重要的。因此,如果我们理解了控制行为的概率,就可以使用马尔科夫链计算变化的长期趋势。希望通过介绍一些蒙特卡洛模拟和马尔科夫链,可以使你对 MCMC 方法的零数学解释有更直观的理解。回到原来的问题,即评估平均身高的后验分布:这个平均身高的后验分布的实例没有基于真实数据。我们知道后验分布在某种程度上处于先验分布和可能性分布的范围内,但无论如何都无法直接计算。使用 MCMC 方法,我们可以有效地从后验分布中提取样本,然后计算统计特征,例如提取样本的平均值。首先,MCMC 方法选择一个随机参数值。模拟过程中会持续生成随机的值(即蒙特卡洛部分),但服从某些能生成更好参数值的规则。即对于一对参数值,可以通过给定先验信度计算每个值解释数据的有效性,从而确定哪个值更好。我们会将更好的参数值以及由这个值的解释数据有效性决定的特定概率添加到参数值的链中(即马尔科夫链部分)。为了可视化地解释上述过程,首先强调一下,一个分布的特定值的高度代表的是观察到该值的概率。因此,参数值(x 轴)对应的概率(y 轴)可能或高或低。对于单个参数,MCMC 方法会从随机在 x 轴上采样开始。红点表征随机参数采样。由于随机采样服从固定的概率,它们倾向于经过一段时间后收敛于参数的高概率区域:蓝点表示当采样收敛之后,经过任意时间的随机采样。注意:垂直堆叠这些点仅仅是为了说明目的。收敛出现之后,MCMC 采样会得到作为后验分布样本的一系列点。用这些点画直方图,然后你可以计算任何感兴趣的统计特征:通过 MCMC 模拟生成的样本集合计算的任何统计特征,都是对真实后验分布的统计特征的最佳近似。MCMC 方法也可以用于评估多于一个参数的后验分布(例如,人类身高和体重)。对于 n 个参数,在 n 维空间中存在高概率的区域,其中特定的参数值集合可以更有效地解释数据。因此,我认为 MCMC 方法的本质,就是在一个概率空间中进行随机采样以近似后验分布。原文链接:https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50机器之心推出「Synced Machine Intelligence Awards」2017,希望通过四大奖项记录这一年人工智能的发展与进步,传递行业启示性价值。来自微信
一份数学小白也能读懂的「马尔可夫链蒙特卡洛方法」入门指南 机器之心2017年12月24日12:46作者:Ben Shaver机器之心编译参与:黄小天、刘晓坤在众多经典的贝叶斯方法中,马尔可夫链蒙特卡洛(MCMC)由于包含大量数学知识,且计算量很大,而显得格外特别。本文反其道而行之,试图通过通俗易懂且不包含数学语言的方法,帮助读者对 MCMC 有一个直观的理解,使得毫无数学基础的人搞明白 MCMC。在我们中的很多人看来,贝叶斯统计学家不是巫术师,就是完全主观的胡说八道者。在贝叶斯经典方法中,马尔可夫链蒙特卡洛(Markov chain Monte Carlo/MCMC)尤其神秘,其中数学很多,计算量很大,但其背后原理与数据科学有诸多相似之处,并可阐释清楚,使得毫无数学基础的人搞明白 MCMC。这正是本文的目标。那么,到底什么是 MCMC 方法?一言以蔽之:MCMC 通过在概率空间中随机采样以近似兴趣参数(parameter of interest)的后验分布。我将在本文中做出简短明了的解释,并且不借助任何数学知识。首先,解释重要的术语。「兴趣参数」(parameter of interest)可以总结我们感兴趣现象的一些数字。我们通常使用统计学评估参数,比如,如果想要了解成年人的身高,我们的兴趣参数可以是精确到英寸的平均身高。「分布」是参数的每个可能值、以及我们有多大可能观察每个参数的数学表征,其最著名的实例是钟形曲线:在贝叶斯统计学中,分布还有另外一种解释。贝叶斯不是仅仅表征一个参数值以及每个参数有多大可能是真值,而是把分布看作是我们对参数的「信念」。因此,钟形曲线表明我们非常确定参数值相当接近于零,但是我们认为在一定程度上真值高于或低于该值的可能性是相等的。事实上,人的身高确实遵从一个正态曲线,因此我们假定平均身高的真值符合钟形曲线,如下所示:很明显,上图表征是巨人的身高分布,因为据图可知,最有可能的平均身高是 6'2"(但他们也并非超级自信)。让我们假设其中某个人后来收集到一些数据,并且观察了身高在 5"和 6"之间的一些人。我们可以用另一条正态曲线表征下面的数据,该曲线表明了哪些平均身高值能最好地解释这些数据:在贝叶斯统计中,表征我们对参数信念的分布被称为「先验分布」,因为它在我们看到任何数据之前捕捉到了我们的信念。「可能性分布」(likelihood distribution)通过表征一系列参数值以及伴随的每个参数值解释观察数据的可能性,以总结数据之中的信息。评估最大化可能性分布的参数值只是回答这一问题:什么参数值会使我们更可能观察到已经观察过的数据?如果没有先验信念,我们可能无法对此作出评估。但是,贝叶斯分析的关键是结合先验与可能性分布以确定后验分布。它可以告诉我们哪个参数值最大化了观察到已观察过的特定数据的概率,并把先验信念考虑在内。在我们的实例中,后验分布如下所示:如上所示,红线表征后验分布。你可以将其看作先验和可能性分布的一种平均值。由于先验分布较小且更加分散,它表征了一组关于平均身高真值的「不太确定」的信念。同时,可能性分布在相对较窄的范围内总结数据,因此它表征了对真参数值的「更确定」的猜测。当先验与可能性分布结合在一起,数据(由可能性分布表征)主导了假定存在于这些巨人之中的个体的先验弱信念。尽管该个体依然认为平均身高比数据告诉他的稍高一些,但是他非常可能被数据说服。在两条钟形曲线的情况下,求解后验分布非常容易。有一个结合了两者的简单等式。但是如果我们的先验和可能性分布表现很差呢?有时使用非简化的形状建模数据或先验信念时是最精确的。如果可能性分布需要带有两个峰值的分布才能得到最好地表征呢?并且出于某些原因我们想要解释一些非常奇怪的先验分布?通过手动绘制一个丑陋的先验分布,我已可视化了该情景,如下所示:可视化由 Matplotlib 渲染,并使用 MS Paint 做了改善如前所述,存在一些后验分布,它给出了每个参数值的可能性分布。但是很难得到完整的分布,也无法解析地求解。这就是使用 MCMC 方法的时候了。MCMC 允许我们在无法直接计算的情况下评估后验分布的形状。为了理解其工作原理,我将首先介绍蒙特卡洛模拟(Monte Carlo simulation),接着讨论马尔可夫链。蒙特卡洛模拟只是一种通过不断地生成随机数来评估固定参数的方法。通过生成随机数并对其做一些计算,蒙特卡洛模拟给出了一个参数的近似值(其中直接计算是不可能的或者计算量过大)。假设我们想评估下图中的圆圈面积:由于圆在边长为 10 英寸的正方形之内,所以通过简单计算可知其面积为 78.5 平方英寸。但是,如果我们随机地在正方形之内放置 20 个点,接着我们计算点落在圆内的比例,并乘以正方形的面积,所得结果非常近似于圆圈面积。由于 15 个点落在了圆内,那么圆的面积可以近似地为 75 平方英寸,对于只有 20 个随机点的蒙特卡洛模拟来说,结果并不差。现在,假设我们想要计算下图中由蝙蝠侠方程(Batman Equation)绘制的图形的面积:我们从来没有学过一个方程可以求这样的面积。不管怎样,通过随机地放入随机点,蒙特卡洛模拟可以相当容易地为该面积提供一个近似值。蒙特卡洛模拟不只用于估算复杂形状的面积。通过生成大量随机数字,它还可用于建模非常复杂的过程。实际上,蒙特卡洛模拟还可以预测天气,或者评估选举获胜的概率。理解 MCMC 方法的第二个要素是马尔科夫链(Markov chains)。马尔科夫链由存在概率相关性的事件的序列构成。每个事件源于一个结果集合,根据一个固定的概率集合,每个结果决定了下一个将出现的结果。马尔科夫链的一个重要特征是「无记忆性」:可能需要用于预测下一个时间的一切都已经包含在当前的状态中,从事件的历史中得不到任何新信息。例如 Chutes and Ladders 这个游戏就展示了这种无记忆性,或者说马尔科夫性,但在现实世界中很少事物是这种性质的。尽管如此,马尔科夫链也是理解现实世界的强大工具。在十九世纪,人们观察到钟形曲线在自然中是一种很常见的模式。(我们注意到,例如,人类的身高服从钟形曲线分布。)Galton Boards 曾通过将弹珠坠落并通过布满木钉的板模拟了重复随机事件的平均值,在弹珠的最终数量分布中重现了钟形曲线:俄罗斯数学家和神学家 Pavel Nekrasov 认为钟形曲线,或者更一般的说,大数规律只不过是小孩子的游戏和普通的谜题中的伪假象,其中每个事件之间都是完全独立的。他认为现实世界中的互相依赖的事件,例如人类行为,并不遵循漂亮的数学模式或分布。Andrey Markov(马尔科夫链正是以他的名字命名)试图证明非独立的事件可能也遵循特定的模式。他的其中一个最著名的例子是从一份俄罗斯诗歌作品中数出几千个两字符对(two-character pairs)。他使用这些两字符对计算了每个字符的条件概率。即,给定一个确定的上述字母或空白,关于下一个字母将是 A、T 或者空白等,存在一个确定的概率。通过这些概率,Markov 可以模拟一个任意的长字符序列。这就是马尔科夫链。虽然早先的几个字符很大程度上依赖于初始字符的选择,Markov 表明在长字符序列中,字符的分布会出现特定的模式。因此,即使是互相依赖的事件,如果服从固定的概率分布,将遵循平均水平的模式。举一个更有意义的例子,假设你住在一个有 5 个房间的房子里,里面有一个卧室、浴室、客厅、厨房、饭厅。然后我们收集一些数据,假定只需要当前你所处的房间和相应的时间就可以预测下一个你所处的房间的概率。例如,如果你在厨房,你有 30% 的概率会留在厨房,有 30% 的概率会走到饭厅,有 20% 的概率会走到客厅,有 10% 的概率会走到浴室,以及有 10% 的概率会走到卧室。使用每个房间的概率集合,我们可以构建一个关于你接下来要去的房间的预测链。如果想预测一个人处于厨房之后所在的房间,基于几个状态而做出预测可能有效。但由于我们的预测仅仅基于一个人在房子中的单次观察,可以合理地认为预测结果是不够好的。例如,如果一个人从卧室走到浴室,相比从厨房走到浴室的情况,他更可能会返回原来的房间。因此,马尔科夫链并不真正适用于现实世界。然而,通过迭代运行马尔科夫链数千次,确实能给出关于你接下来可能所处的房间的长期预测。更重要的是,这个预测并不受这个人起始所处的房间的影响。对此可以直观地理解为:在模拟和描述长期过程(或普遍情况)一个人所处房间的概率时,时间因素是不重要的。因此,如果我们理解了控制行为的概率,就可以使用马尔科夫链计算变化的长期趋势。希望通过介绍一些蒙特卡洛模拟和马尔科夫链,可以使你对 MCMC 方法的零数学解释有更直观的理解。回到原来的问题,即评估平均身高的后验分布:这个平均身高的后验分布的实例没有基于真实数据。我们知道后验分布在某种程度上处于先验分布和可能性分布的范围内,但无论如何都无法直接计算。使用 MCMC 方法,我们可以有效地从后验分布中提取样本,然后计算统计特征,例如提取样本的平均值。首先,MCMC 方法选择一个随机参数值。模拟过程中会持续生成随机的值(即蒙特卡洛部分),但服从某些能生成更好参数值的规则。即对于一对参数值,可以通过给定先验信度计算每个值解释数据的有效性,从而确定哪个值更好。我们会将更好的参数值以及由这个值的解释数据有效性决定的特定概率添加到参数值的链中(即马尔科夫链部分)。为了可视化地解释上述过程,首先强调一下,一个分布的特定值的高度代表的是观察到该值的概率。因此,参数值(x 轴)对应的概率(y 轴)可能或高或低。对于单个参数,MCMC 方法会从随机在 x 轴上采样开始。红点表征随机参数采样。由于随机采样服从固定的概率,它们倾向于经过一段时间后收敛于参数的高概率区域:蓝点表示当采样收敛之后,经过任意时间的随机采样。注意:垂直堆叠这些点仅仅是为了说明目的。收敛出现之后,MCMC 采样会得到作为后验分布样本的一系列点。用这些点画直方图,然后你可以计算任何感兴趣的统计特征:通过 MCMC 模拟生成的样本集合计算的任何统计特征,都是对真实后验分布的统计特征的最佳近似。MCMC 方法也可以用于评估多于一个参数的后验分布(例如,人类身高和体重)。对于 n 个参数,在 n 维空间中存在高概率的区域,其中特定的参数值集合可以更有效地解释数据。因此,我认为 MCMC 方法的本质,就是在一个概率空间中进行随机采样以近似后验分布。原文链接:https://towardsdatascience.com/a-zero-math-introduction-to-markov-chain-monte-carlo-methods-dcba889e0c50机器之心推出「Synced Machine Intelligence Awards」2017,希望通过四大奖项记录这一年人工智能的发展与进步,传递行业启示性价值。来自微信 -
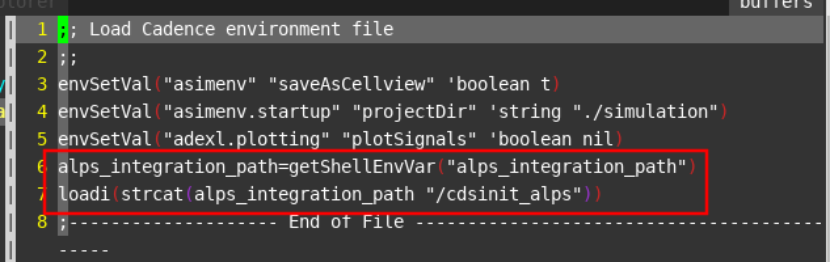
 virtuoso和empyrean alps模拟仿真和混仿教程 1 virtuoso+alps模拟仿真在virtuoso 可以通过spectre 仿真环境基础上。参考网页1).设置环境变量,比如csh 环境setenv alps_integration_path /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds加载工具:module load cadence/spectre/SPECTRE191ISR8module load cadence/virtuoso/IC618ISR13module load cadence/xcelium/18.03.001module load empyrean/alps/alpsIC_2023.03.hf22). 复制配置文件到virtuoso 项目路径,比如cp /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds/.cdsinit /project/cim01t28a0/verification/bennyhe/ver/ut/cim/sim/hspice/.cdsinit 文件如下:3 )启动virtuoso 并仿真加载alps 信息打开之前spectre 仿真的 schematic启动ADE Lsetup->simulator/Directory/Host 选择spectresetup->environment 勾上Use ALPSALPS是纯模拟的仿真器ALPSCS 是数模混合仿真器User Command-Line Options可以填写alps 工具参数比如启动32核比如其他设置和使用spectre 仿真一样需要观察的信号点击会出现log 和波形2 virtuoso+alps数模混合仿真在virtuoso 可以通过spectre 仿真环境基础上。参考网页1).设置环境变量,比如csh 环境setenv alps_integration_path /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds加载工具:module load cadence/spectre/SPECTRE191ISR8module load cadence/virtuoso/IC618ISR13module load cadence/xcelium/18.03.001module load empyrean/alps/alpsIC_2023.03.hf23). 复制配置文件到virtuoso 项目路径,比如cp /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds/.cdsinit /project/cim01t28a0/verification/bennyhe/ver/ut/cim/sim/cosim/.cdsinit 文件如下:启动virtuoso 并仿真加载alps 信息。选择config界面弹出这个窗口可以设置数字单元为External HDL然后启动ADE L在ADE L界面setup->simulator/Directory/Host 选择spectresetup->environment 勾上Use ALPSCS模拟仿真设置模拟需要观察的信号在回到选择ALPS AMS Setup,勾选IEExtend 页面选择 A2D、D2A数字模拟电压转换关系Extend 界面的Save signals to waveform,设置为* 表示保存所有的数字信号Arguments 页面选择数字仿真器Digital Solver 为nc(cadence 的xrun)保存的analog 和 digital的波形 ps/fsdb 、vcd/fsdb,在这个demo中选择ps、vcd, fsdb的波形需要和verdi结合(需要单独的配置),在ALPS Command Options中勾上,删除默认的一些参数,有必要的情况也添加alpscs 的仿真参数,在这个demo 中没有添加然后在run界面 选择会显示以及调用xrun的过程产生的数字波形的路径./simulation/inv_tb/spectre/config/netlist/alps_m.adp.sim.vcd可以使用simvision或者verdi、dve或者empyrean 的 iwave 打开vcd波形这里以simvision 为例子
virtuoso和empyrean alps模拟仿真和混仿教程 1 virtuoso+alps模拟仿真在virtuoso 可以通过spectre 仿真环境基础上。参考网页1).设置环境变量,比如csh 环境setenv alps_integration_path /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds加载工具:module load cadence/spectre/SPECTRE191ISR8module load cadence/virtuoso/IC618ISR13module load cadence/xcelium/18.03.001module load empyrean/alps/alpsIC_2023.03.hf22). 复制配置文件到virtuoso 项目路径,比如cp /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds/.cdsinit /project/cim01t28a0/verification/bennyhe/ver/ut/cim/sim/hspice/.cdsinit 文件如下:3 )启动virtuoso 并仿真加载alps 信息打开之前spectre 仿真的 schematic启动ADE Lsetup->simulator/Directory/Host 选择spectresetup->environment 勾上Use ALPSALPS是纯模拟的仿真器ALPSCS 是数模混合仿真器User Command-Line Options可以填写alps 工具参数比如启动32核比如其他设置和使用spectre 仿真一样需要观察的信号点击会出现log 和波形2 virtuoso+alps数模混合仿真在virtuoso 可以通过spectre 仿真环境基础上。参考网页1).设置环境变量,比如csh 环境setenv alps_integration_path /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds加载工具:module load cadence/spectre/SPECTRE191ISR8module load cadence/virtuoso/IC618ISR13module load cadence/xcelium/18.03.001module load empyrean/alps/alpsIC_2023.03.hf23). 复制配置文件到virtuoso 项目路径,比如cp /data/ver/superbench/v2_0_beta/tool/integration_alpscs/cds/.cdsinit /project/cim01t28a0/verification/bennyhe/ver/ut/cim/sim/cosim/.cdsinit 文件如下:启动virtuoso 并仿真加载alps 信息。选择config界面弹出这个窗口可以设置数字单元为External HDL然后启动ADE L在ADE L界面setup->simulator/Directory/Host 选择spectresetup->environment 勾上Use ALPSCS模拟仿真设置模拟需要观察的信号在回到选择ALPS AMS Setup,勾选IEExtend 页面选择 A2D、D2A数字模拟电压转换关系Extend 界面的Save signals to waveform,设置为* 表示保存所有的数字信号Arguments 页面选择数字仿真器Digital Solver 为nc(cadence 的xrun)保存的analog 和 digital的波形 ps/fsdb 、vcd/fsdb,在这个demo中选择ps、vcd, fsdb的波形需要和verdi结合(需要单独的配置),在ALPS Command Options中勾上,删除默认的一些参数,有必要的情况也添加alpscs 的仿真参数,在这个demo 中没有添加然后在run界面 选择会显示以及调用xrun的过程产生的数字波形的路径./simulation/inv_tb/spectre/config/netlist/alps_m.adp.sim.vcd可以使用simvision或者verdi、dve或者empyrean 的 iwave 打开vcd波形这里以simvision 为例子 -
 Verilog-AMS 知识汇总 verilog-AMS数据类型 --- wrealWREAL 是Verilog-AMS支持的一种新的数值模型。WREAL的特殊之处在于它使用有限的浮点数值的点来模拟一条电路工作曲线。而SPICE和Verilog-A的计算结果是一条理论上可以无限精度,包含无限点的的曲线。从某种程度上,WREAL的实现方式类似于Fast-Spice的查表点工作模式,其目的是进一步简化仿真,从而支持更大规模的模拟系统仿真。 使用WREAL的最大好处是速度快。使用WREAL变量的模型在计算的时候无需使用SPICE迭代运算。它使用的是比较简单的,直接推导的函数来模仿模拟电路真正的工作情况。 相比SPICE和Verilog-A的模型必须使用SPICE仿真器的迭代运算,WREAL仿真器使用离散事件触发,就像数字仿真器那样。这给WREAL的计算上带来极大的速度优势。但同时,离散的计算模式使得WREA模型在含有反馈的电路中无法给出准确的结果。在普通电路中它也需要牺牲输出的精度。所以,WREAL并不适用于需要精确度量的模拟电路的模型中。 WREAL的一个问题是,它需要对真正的模拟电路的行为有一个非常好的预测。因为,WREAL的所有计算都是前向的,我们想要用这些前向计算来模拟SPICE仿真器迭代结算的结果,就需要对实际电路工作情况有个很好的了解。然而,模型通常在设计阶段的前期实现,而此时通常不会有很好的对真实电路的预测。如果WREAL模型无法很好的体现SPICE仿真器对真实电路的仿真结果,那模型的意义就不大了。亦或需要在设计后期随着真实电路的开发修改模型,这样就会牺牲一些研发的时间。 有一些相关的研究正在进行中,比如利用简单的电路生成WREAL模型,这样可以作为未来新项目系统的起始WREAL模型。也有一些研究包括迭代WREAL和真实电路仿真,这样可以自动修改WREAL模型等等。但不管怎么,对于WREAL在大规模需要精度的验证中的使用,还是需要一定考虑。 一、端口(Port) Port(端口),也被称为引脚或端子,被用来连接模块到其他模块。因此,端口就是电线。简单连接的端口声明是连接声明,其中关键字wire被以下方向说明符之一替换:input、output或inout。例如: module inv (out, in); output out; input in;assign out = ~in;endmodulemodule mux (out, in0, in1, sel); output [7:0] out; input [7:0] in0, in1; input sel;assign out = sel ? in1 : in0;endmodule 对于其他类型的连接,或者寄存器(寄存器只能作为输出声明),声明的前面简单地加上方向说明符: module counter (out, clk); output reg [3:0] out;initial out = 0;always @(posedge ckl) out = out + 1;endmodule 默认情况下,多位端口的内容被解释为无符号数(值被解释为正二进制数)。可以明确指定数字是被解释为有符号数还是无符号数,如下所示: input unsigned [3:0] gain;input signed [6:0] offset;在这种情况下,增益是无符号的,而偏移量是有符号的,这意味着它被解释为有符号的双补数。因此,如果增益= 4'bF,则其值解释为15,如果offset = 7'b7FF,则其值解释为-1。 If it is necessary to apply a discipline to a port, the port declaration should be repeated with direction specifier replaced by the discipline. For example: module buffer (out, in); output out; input in; electrical out, in;analog V(out) <+ V(in);endmodule Verilog还支持连续信号总线和wreal(必须声明为总线而不是数组): module mux (out, in, sel); output out; input [1:0] in; input sel; electrical out; electrical [1:0] in;analog begin @(sel); V(out) <+ transition(sel === 0, 0, 100n)*V(in[0]); V(out) <+ transition(sel === 1, 0, 100n)*V(in[1]);endendmodulemodule mux (out, in, sel); output wreal out; input wreal [1:0] in; input sel;assign out = sel ? in[1] : in[0];endmodule Note:The Cadence simulator does not seem to follow the standard when it comes to declaring buses of wreals. With the Cadence simulator you should declare buses of wreals as arrays rather than as buses: module mux (out, in, sel); output wreal out; input wreal in[1:0]; input sel;assign out = sel ? in[1] : in[0];endmodule———————————————— 版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 原文链接:https://blog.csdn.net/gsjthxy/article/details/107618649
Verilog-AMS 知识汇总 verilog-AMS数据类型 --- wrealWREAL 是Verilog-AMS支持的一种新的数值模型。WREAL的特殊之处在于它使用有限的浮点数值的点来模拟一条电路工作曲线。而SPICE和Verilog-A的计算结果是一条理论上可以无限精度,包含无限点的的曲线。从某种程度上,WREAL的实现方式类似于Fast-Spice的查表点工作模式,其目的是进一步简化仿真,从而支持更大规模的模拟系统仿真。 使用WREAL的最大好处是速度快。使用WREAL变量的模型在计算的时候无需使用SPICE迭代运算。它使用的是比较简单的,直接推导的函数来模仿模拟电路真正的工作情况。 相比SPICE和Verilog-A的模型必须使用SPICE仿真器的迭代运算,WREAL仿真器使用离散事件触发,就像数字仿真器那样。这给WREAL的计算上带来极大的速度优势。但同时,离散的计算模式使得WREA模型在含有反馈的电路中无法给出准确的结果。在普通电路中它也需要牺牲输出的精度。所以,WREAL并不适用于需要精确度量的模拟电路的模型中。 WREAL的一个问题是,它需要对真正的模拟电路的行为有一个非常好的预测。因为,WREAL的所有计算都是前向的,我们想要用这些前向计算来模拟SPICE仿真器迭代结算的结果,就需要对实际电路工作情况有个很好的了解。然而,模型通常在设计阶段的前期实现,而此时通常不会有很好的对真实电路的预测。如果WREAL模型无法很好的体现SPICE仿真器对真实电路的仿真结果,那模型的意义就不大了。亦或需要在设计后期随着真实电路的开发修改模型,这样就会牺牲一些研发的时间。 有一些相关的研究正在进行中,比如利用简单的电路生成WREAL模型,这样可以作为未来新项目系统的起始WREAL模型。也有一些研究包括迭代WREAL和真实电路仿真,这样可以自动修改WREAL模型等等。但不管怎么,对于WREAL在大规模需要精度的验证中的使用,还是需要一定考虑。 一、端口(Port) Port(端口),也被称为引脚或端子,被用来连接模块到其他模块。因此,端口就是电线。简单连接的端口声明是连接声明,其中关键字wire被以下方向说明符之一替换:input、output或inout。例如: module inv (out, in); output out; input in;assign out = ~in;endmodulemodule mux (out, in0, in1, sel); output [7:0] out; input [7:0] in0, in1; input sel;assign out = sel ? in1 : in0;endmodule 对于其他类型的连接,或者寄存器(寄存器只能作为输出声明),声明的前面简单地加上方向说明符: module counter (out, clk); output reg [3:0] out;initial out = 0;always @(posedge ckl) out = out + 1;endmodule 默认情况下,多位端口的内容被解释为无符号数(值被解释为正二进制数)。可以明确指定数字是被解释为有符号数还是无符号数,如下所示: input unsigned [3:0] gain;input signed [6:0] offset;在这种情况下,增益是无符号的,而偏移量是有符号的,这意味着它被解释为有符号的双补数。因此,如果增益= 4'bF,则其值解释为15,如果offset = 7'b7FF,则其值解释为-1。 If it is necessary to apply a discipline to a port, the port declaration should be repeated with direction specifier replaced by the discipline. For example: module buffer (out, in); output out; input in; electrical out, in;analog V(out) <+ V(in);endmodule Verilog还支持连续信号总线和wreal(必须声明为总线而不是数组): module mux (out, in, sel); output out; input [1:0] in; input sel; electrical out; electrical [1:0] in;analog begin @(sel); V(out) <+ transition(sel === 0, 0, 100n)*V(in[0]); V(out) <+ transition(sel === 1, 0, 100n)*V(in[1]);endendmodulemodule mux (out, in, sel); output wreal out; input wreal [1:0] in; input sel;assign out = sel ? in[1] : in[0];endmodule Note:The Cadence simulator does not seem to follow the standard when it comes to declaring buses of wreals. With the Cadence simulator you should declare buses of wreals as arrays rather than as buses: module mux (out, in, sel); output wreal out; input wreal in[1:0]; input sel;assign out = sel ? in[1] : in[0];endmodule———————————————— 版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 原文链接:https://blog.csdn.net/gsjthxy/article/details/107618649 -
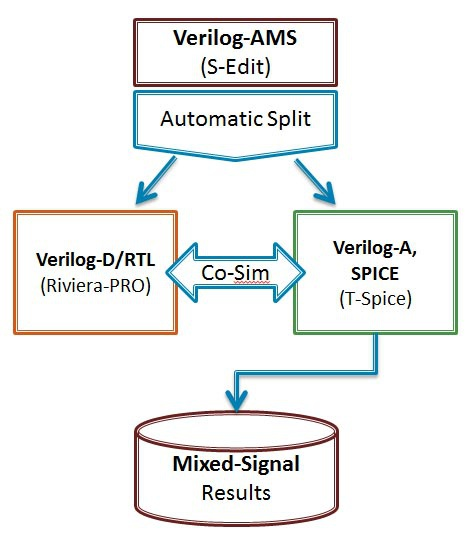
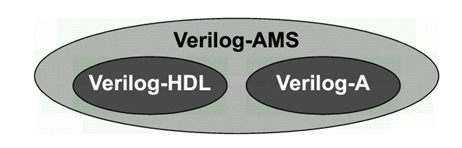
 Verilog-AMS Verilog-A介绍 最近浅学了一下Verilog-AMS和Verilog-A的语法,记录一下自己理解:.Verilog-A是Verilog-AMS的子集,Verilog-A是只对analog电路进行建模的(运行基于Spice仿真器),而Verilog-AMS则可以对mixed- signal电路进行建模,包括了数字Verilog和Veirlog-A的语法 (运行基于 AMS混合信号仿真器).对于Verilog-A来说,其端口都是电器属性的,即类似于你从Spice里看到的那些模型一样;.对于Verilog-AMS来说,可以有logic类型的数字端口输入,然后electrical类型的模拟端口输出等等;.Verilog-AMS/A 可以从行为级和电路级对电路进行建模,简化了对于系统电路仿真时的复杂性;veirlog-AMS/Verilog-A中的关键概念:.分立信号转化为连续的信号 (对于数字只有0,1两种状态,但转化为连续信号,0->1过程值也会存在);.事件发生来触发信号变化(基于添加时间戳)(需解决设置的变量在事件未触发之前的初值问题);.在Verilog-A中,要时刻考虑Vth的特性,注意基于Verilog-A的model写法!.事件触发原理:在连续仿真器中,在发生事件处放置一个时间标记,从而将离散的仿真连续化;.model概念,branch概念,testbench概念(类似于verilog);一些关键代码:0. Verilog-A的阈值电压检测标准代码 (基于反相器):module inverter(out, in):output out;input in;electrical out, in;integer d_in; analog begin @(cross(V(in) - 0.5*V(vdd))) //穿越阈值电压写法(event statement),作用是在这个点建立时间戳,方便仿真器进行捕捉,否则捕捉不到这里发生的突变 ; //空白行,不在event发生时执行特定命令 d_in = V(in) > 0.5*V(vdd); //建立方波 V(out) <+ transition(!d_in, 0, 10n)*V(vdd); //用transition进行smooth处理 end endmodule.Model DAC (关键:electrical digital input -> (Vth) -> integer -> electrical analog differential output)module dac (out_p, out_n, in, clock, enable, vdda, gnda); output out_p, out_n; electrical out_p, out_n; input [7:0] in; electrical [7:0] in; input clock; electrical clock; input enable; electrical enable; input vdda; electrical vdda; input gnda; electrical gnda; integer code, en; real value;genvar i; analog begin // convert the input to a signed integer on positive clock edge @(cross(V(clock) - V(vdda)/2), +1) begin code = 0; for (i = 0; i < 8; i = i + 1) begin @(cross(V(in[i]) - V(vdda)/2)); if (V(in[i]) > V(vdda)/2) code = code + (1 << i); if (code >= 128) code = code - 256; value = code/256.0; end // reset output value when disabled @(cross(V(enable) - V(vdda)/2)) ; if (V(enable) < V(vdda)/2) value = 0; // drive the differential output V(out_p) <+ V(vdda)/2 + transition(value/2, 0, 10n); V(out_n) <+ V(vdda)/2 - transition(value/2, 0, 10n); end endmodule2. Model ADC (关键:electrical analog input -> (vth) -> integer -> electrical digital output)module adc (out, in, clk); output [5:0] out; input in, clk; electrical [5:0] out; electrical in, clk; parameter real vh = 1; parameter real vth = vh/2; parameter real tt = 100n from (0:inf); integer result; genvar i; analog begin @(cross(V(clk) - vth, +1)) begin result = 64*(V(in)+1)/2; if (result > 63) result = 63; else if (result < 0) result = 0; end for (i=0; i<6; i=i+1) V(out[i]) <+ transition(result & (1<<i) ? vh : 0, 0, tt); end endmodule3. Model Multiplexer: (关键:[3:0] sel 可以直接放入 @()中)module(out, in, sel); output out; electrical out; input [3:0] in; electrical [3:0] in; input [3:0] sel; logic [3:0] sel; analog begin @(sel) ; V(out) <+ V(in[0])*transition(sel === 0, 0, 100n); V(out) <+ V(in[1])*transition(sel === 1, 0, 100n); V(out) <+ V(in[2])*transition(sel === 2, 0, 100n); V(out) <+ V(in[3])*transition(sel === 3, 0, 100n); end endmodule4. 对于Cadence语法限制的标准处理方法:(Unfortunately, the Cadence simulator places unreasonable restrictions on event expressions in the analog block. Specifically, any digital signals used in an analog event expression must be preceded by either the posedge or negedge qualifiers. Thus, the model must be modified when intended for the Cadence simulator: )module cp (out, u, d): output out; electrical out; input u, d; logic u, d; reg sync = 0; always @(u or d) sync <= !sync; analog begin @(posedge sync or negedge sync) ; I(out) <+ 10u*(transition(d, 0, 1n) - transition(u, 0, 1n)); end endmodulean example of writing in Cadence:Cadence’s AMS simulator only supports discrete transitions filtered through posedge or negedge. Putting a discrete wire, discrete variable, or named event directly in a continuous event statement is not supported (as of 2014).real vgain;always @(gain) vgain = pow(10, (gain - 32.0)/20); real voffset;always @(offset) voffset = 1m*offset; reg break = 0;always @(vgain or voffset or en) break <= break; analog begin @(posedge break or negedge break) ; V(out) <+ transition(en ? vgain : 0, 0, 100n) * V(in) + voffset; endWith Cadence’s simulator, you can use the following for modeling multiplexers:module(out, in, sel); output out; electrical out; input [3:0] in; electrical [3:0] in; input [3:0] sel; logic [3:0] sel; reg sync = 0; always @(sel) sync <= !sync; analog begin @(posedge sync or negedge sync) ; V(out) <+ V(in[0])*transition(sel === 0, 0, 100n); V(out) <+ V(in[1])*transition(sel === 1, 0, 100n); V(out) <+ V(in[2])*transition(sel === 2, 0, 100n); V(out) <+ V(in[3])*transition(sel === 3, 0, 100n); end endmoduleTo implement a Verilog-A version of a multiplexer:module(out, in, sel); output out; electrical out; input [3:0] in; electrical [3:0] in; input [3:0] sel; logic [3:0] sel; parameter real vdd = 2.5; integer SEL; genvar i; analog begin // convert the input to an integer SEL = 0; for (i = 0; i < 2; i = i + 1) begin @(cross(V(sel[i]) - vdd/2)); if (V(sel[i]) > vdd/2) SEL = SEL + (1 << i); end V(out) <+ V(in[0])*transition(SEL == 0, 0, 100n); V(out) <+ V(in[1])*transition(SEL == 1, 0, 100n); V(out) <+ V(in[2])*transition(SEL == 2, 0, 100n); V(out) <+ V(in[3])*transition(SEL == 3, 0, 100n); end endmodule
Verilog-AMS Verilog-A介绍 最近浅学了一下Verilog-AMS和Verilog-A的语法,记录一下自己理解:.Verilog-A是Verilog-AMS的子集,Verilog-A是只对analog电路进行建模的(运行基于Spice仿真器),而Verilog-AMS则可以对mixed- signal电路进行建模,包括了数字Verilog和Veirlog-A的语法 (运行基于 AMS混合信号仿真器).对于Verilog-A来说,其端口都是电器属性的,即类似于你从Spice里看到的那些模型一样;.对于Verilog-AMS来说,可以有logic类型的数字端口输入,然后electrical类型的模拟端口输出等等;.Verilog-AMS/A 可以从行为级和电路级对电路进行建模,简化了对于系统电路仿真时的复杂性;veirlog-AMS/Verilog-A中的关键概念:.分立信号转化为连续的信号 (对于数字只有0,1两种状态,但转化为连续信号,0->1过程值也会存在);.事件发生来触发信号变化(基于添加时间戳)(需解决设置的变量在事件未触发之前的初值问题);.在Verilog-A中,要时刻考虑Vth的特性,注意基于Verilog-A的model写法!.事件触发原理:在连续仿真器中,在发生事件处放置一个时间标记,从而将离散的仿真连续化;.model概念,branch概念,testbench概念(类似于verilog);一些关键代码:0. Verilog-A的阈值电压检测标准代码 (基于反相器):module inverter(out, in):output out;input in;electrical out, in;integer d_in; analog begin @(cross(V(in) - 0.5*V(vdd))) //穿越阈值电压写法(event statement),作用是在这个点建立时间戳,方便仿真器进行捕捉,否则捕捉不到这里发生的突变 ; //空白行,不在event发生时执行特定命令 d_in = V(in) > 0.5*V(vdd); //建立方波 V(out) <+ transition(!d_in, 0, 10n)*V(vdd); //用transition进行smooth处理 end endmodule.Model DAC (关键:electrical digital input -> (Vth) -> integer -> electrical analog differential output)module dac (out_p, out_n, in, clock, enable, vdda, gnda); output out_p, out_n; electrical out_p, out_n; input [7:0] in; electrical [7:0] in; input clock; electrical clock; input enable; electrical enable; input vdda; electrical vdda; input gnda; electrical gnda; integer code, en; real value;genvar i; analog begin // convert the input to a signed integer on positive clock edge @(cross(V(clock) - V(vdda)/2), +1) begin code = 0; for (i = 0; i < 8; i = i + 1) begin @(cross(V(in[i]) - V(vdda)/2)); if (V(in[i]) > V(vdda)/2) code = code + (1 << i); if (code >= 128) code = code - 256; value = code/256.0; end // reset output value when disabled @(cross(V(enable) - V(vdda)/2)) ; if (V(enable) < V(vdda)/2) value = 0; // drive the differential output V(out_p) <+ V(vdda)/2 + transition(value/2, 0, 10n); V(out_n) <+ V(vdda)/2 - transition(value/2, 0, 10n); end endmodule2. Model ADC (关键:electrical analog input -> (vth) -> integer -> electrical digital output)module adc (out, in, clk); output [5:0] out; input in, clk; electrical [5:0] out; electrical in, clk; parameter real vh = 1; parameter real vth = vh/2; parameter real tt = 100n from (0:inf); integer result; genvar i; analog begin @(cross(V(clk) - vth, +1)) begin result = 64*(V(in)+1)/2; if (result > 63) result = 63; else if (result < 0) result = 0; end for (i=0; i<6; i=i+1) V(out[i]) <+ transition(result & (1<<i) ? vh : 0, 0, tt); end endmodule3. Model Multiplexer: (关键:[3:0] sel 可以直接放入 @()中)module(out, in, sel); output out; electrical out; input [3:0] in; electrical [3:0] in; input [3:0] sel; logic [3:0] sel; analog begin @(sel) ; V(out) <+ V(in[0])*transition(sel === 0, 0, 100n); V(out) <+ V(in[1])*transition(sel === 1, 0, 100n); V(out) <+ V(in[2])*transition(sel === 2, 0, 100n); V(out) <+ V(in[3])*transition(sel === 3, 0, 100n); end endmodule4. 对于Cadence语法限制的标准处理方法:(Unfortunately, the Cadence simulator places unreasonable restrictions on event expressions in the analog block. Specifically, any digital signals used in an analog event expression must be preceded by either the posedge or negedge qualifiers. Thus, the model must be modified when intended for the Cadence simulator: )module cp (out, u, d): output out; electrical out; input u, d; logic u, d; reg sync = 0; always @(u or d) sync <= !sync; analog begin @(posedge sync or negedge sync) ; I(out) <+ 10u*(transition(d, 0, 1n) - transition(u, 0, 1n)); end endmodulean example of writing in Cadence:Cadence’s AMS simulator only supports discrete transitions filtered through posedge or negedge. Putting a discrete wire, discrete variable, or named event directly in a continuous event statement is not supported (as of 2014).real vgain;always @(gain) vgain = pow(10, (gain - 32.0)/20); real voffset;always @(offset) voffset = 1m*offset; reg break = 0;always @(vgain or voffset or en) break <= break; analog begin @(posedge break or negedge break) ; V(out) <+ transition(en ? vgain : 0, 0, 100n) * V(in) + voffset; endWith Cadence’s simulator, you can use the following for modeling multiplexers:module(out, in, sel); output out; electrical out; input [3:0] in; electrical [3:0] in; input [3:0] sel; logic [3:0] sel; reg sync = 0; always @(sel) sync <= !sync; analog begin @(posedge sync or negedge sync) ; V(out) <+ V(in[0])*transition(sel === 0, 0, 100n); V(out) <+ V(in[1])*transition(sel === 1, 0, 100n); V(out) <+ V(in[2])*transition(sel === 2, 0, 100n); V(out) <+ V(in[3])*transition(sel === 3, 0, 100n); end endmoduleTo implement a Verilog-A version of a multiplexer:module(out, in, sel); output out; electrical out; input [3:0] in; electrical [3:0] in; input [3:0] sel; logic [3:0] sel; parameter real vdd = 2.5; integer SEL; genvar i; analog begin // convert the input to an integer SEL = 0; for (i = 0; i < 2; i = i + 1) begin @(cross(V(sel[i]) - vdd/2)); if (V(sel[i]) > vdd/2) SEL = SEL + (1 << i); end V(out) <+ V(in[0])*transition(SEL == 0, 0, 100n); V(out) <+ V(in[1])*transition(SEL == 1, 0, 100n); V(out) <+ V(in[2])*transition(SEL == 2, 0, 100n); V(out) <+ V(in[3])*transition(SEL == 3, 0, 100n); end endmodule -
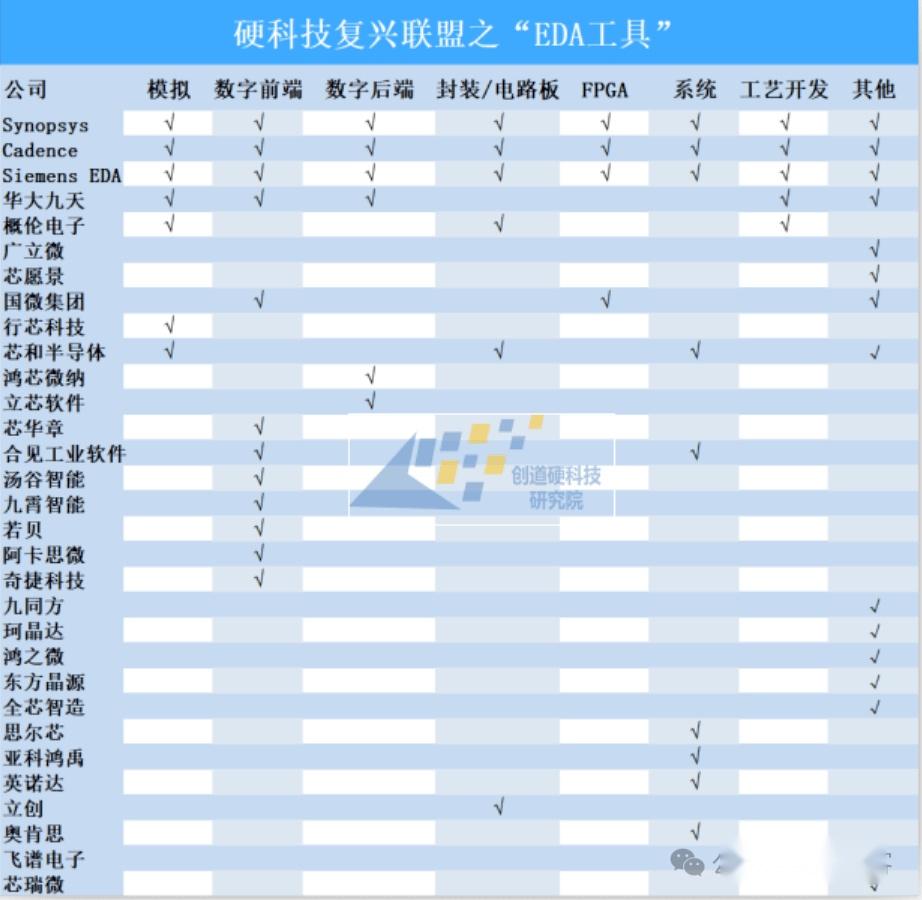
 国产EDA工具厂商汇总与世界三大巨头对比 从国内EDA市场来看,美国三大EDA厂商也占据了主导地位。根据赛迪智库数据显示,2020年Synopsys、Cadence和Seimens EDA三巨头合计占领国内约80%的市场份额,国产EDA厂商的份额仅11.5%,其中华大九天占据了国内EDA市场约6%的市场份额,居本土EDA企业首位。近年来,全球 EDA 市场呈现出稳步增长的态势。根据市场研究机构的数据,2020-2025 年期间,全球 EDA 市场规模持续攀升(见下图 )。2020 年,全球 EDA 市场规模约为 115 亿美元,到 2025 年,预计将达到 157 亿美元,年均复合增长率为 6.4%。这一增长主要得益于 5G、AI、物联网等新兴技术的快速发展,以及全球范围内对高性能、低功耗芯片的需求不断增加。
国产EDA工具厂商汇总与世界三大巨头对比 从国内EDA市场来看,美国三大EDA厂商也占据了主导地位。根据赛迪智库数据显示,2020年Synopsys、Cadence和Seimens EDA三巨头合计占领国内约80%的市场份额,国产EDA厂商的份额仅11.5%,其中华大九天占据了国内EDA市场约6%的市场份额,居本土EDA企业首位。近年来,全球 EDA 市场呈现出稳步增长的态势。根据市场研究机构的数据,2020-2025 年期间,全球 EDA 市场规模持续攀升(见下图 )。2020 年,全球 EDA 市场规模约为 115 亿美元,到 2025 年,预计将达到 157 亿美元,年均复合增长率为 6.4%。这一增长主要得益于 5G、AI、物联网等新兴技术的快速发展,以及全球范围内对高性能、低功耗芯片的需求不断增加。